php组合设计模式(composite pattern)

过十点。

<?php
/*
The composite pattern is about treating the hierarchy of objects as a single object,
through a common interface. Where the objects are composed into three structures
and the client is oblivious to changes in the underlying structure because it only
consumes the common interface.
*/

interface Graphic {
    public function draw();
}

class CompositeGraphic implements Graphic {
    private $graphics = array();

    public function add($graphic) {
        $objId = spl_object_hash($graphic);
        $this->graphics[$objId] = $graphic;
    }

    public function remove($graphic) {
        $objId = spl_object_hash($graphic);
        unset($this->graphics[$objId]);
    }

    public function draw() {
        foreach ($this->graphics as $graphic) {
            $graphic->draw();
        }
    }
}

class Circle implements Graphic {
    public function draw() {
        echo 'draw-Circle<br/>';
    }
}

class Square implements Graphic {
    public function draw() {
        echo 'draw-Square<br/>';
    }
}

class Triangle implements Graphic {
    public function draw() {
        echo 'draw-Triangle<br/>';
    }
}

$circle = new Circle();
$square = new Square();
$triangle = new Triangle();

$compositeObj1 = new CompositeGraphic();
$compositeObj1->add($circle);
$compositeObj1->add($triangle);
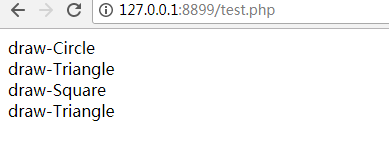
$compositeObj1->draw();

$compositeObj2 = new CompositeGraphic();
$compositeObj2->add($circle);
$compositeObj2->add($square);
$compositeObj2->add($triangle);
$compositeObj2->remove($circle);
$compositeObj2->draw();
?>