P1436 棋盘分割[dp]

题目描述

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

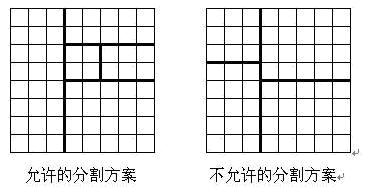
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

解析

$dp[k][i][j][x][y]$表示当前在切第k刀，当前切$(i,j)$为左上角，$(x,y)$为右下角的矩形的最小平方和。

考虑状态转移，一个状态转移到下一个时，它可以继续往两个部分切下去，也就是往两个方向转移。

采用前缀和优化，其中$calc(i,j,x,y)$表示以$(i,j)$为左上角，$(x,y)$为右下角的矩形的和的平方。

\[dp[k][i][j][x][y]=min(dp[k][i][j][x][y],dp[k-1][i'+1][j][x][y]+calc(i,j,i',y),
\\dp[k-1][i][j][x'][y]+calc(x'+1,j,x,y))
\]

\[dp[k][i][j][x][y]=min(dp[k][i][j][x][y],dp[k-1][i][j'+1][x][y]+clac(i,j,x,j'),
\\dp[k-1][i][j][x][y']+calc(i,y',x,y))
\]

初始化显然是切第0刀时，切任意矩形的最小平方和就是不切，就是该矩形的和的平方。

之前的思路和这个稍稍有些不同，我定义dp数组为当前切剩下以$(i,j)$为左上角，$(x,y)$为右下角的矩形的最小平方和，那么就需要四个转移，但是我转移写炸了（摊。

参考代码

#include<iostream>

#include<cstdio>

#include<cstring>

#include<cmath>

#include<algorithm>

#include<string>

#include<cstdlib>

#include<queue>

#include<vector>

#define INF 0x3f3f3f3f

#define PI acos(-1.0)

#define N 11

#define MOD 2520

#define E 1e-12

using namespace std;

int dp[16][N][N][N][N],mp[N][N],n;

inline int read()

{

	int f=1,x=0;char c=getchar();

	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}

	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}

	return x*f;

}

inline int calc(int x1,int y1,int x2,int y2)

{

	if(x1>x2) swap(x1,x2);

	if(y1>y2) swap(y1,y2);

	return (mp[x2][y2]-mp[x1-1][y2]-mp[x2][y1-1]+mp[x1-1][y1-1])*(mp[x2][y2]-mp[x1-1][y2]-mp[x2][y1-1]+mp[x1-1][y1-1]);

}

int main()

{

	n=read();

	memset(dp,0x3f,sizeof(dp));

	memset(dp[0],0,sizeof(dp[0]));

	for(int i=1;i<=8;++i)

		for(int j=1;j<=8;++j){

			dp[0][i][j][i][j]=mp[i][j]=read();

			mp[i][j]+=mp[i-1][j]+mp[i][j-1]-mp[i-1][j-1];

		}

	for(int i=1;i<=8;++i)

		for(int j=1;j<=8;++j)

			for(int x=i;x<=8;++x)

				for(int y=j;y<=8;++y)

					dp[0][i][j][x][y]=calc(i,j,x,y);

	for(int k=1;k<n;++k){

		for(int i=1;i<=8;++i)

			for(int j=1;j<=8;++j)

				for(int x=i;x<=8;++x)

					for(int y=j;y<=8;++y){

						for(int dx=i;dx<=x;++dx)

							dp[k][i][j][x][y]=min(dp[k][i][j][x][y],min(dp[k-1][i][j][dx][y]+calc(dx+1,j,x,y),dp[k-1][dx+1][j][x][y]+calc(i,j,dx,y)));

						for(int dy=j;dy<=y;++dy)

							dp[k][i][j][x][y]=min(dp[k][i][j][x][y],min(dp[k-1][i][j][x][dy]+calc(i,dy+1,x,y),dp[k-1][i][dy+1][x][y]+calc(i,j,x,dy)));

					}

	}

	cout<<dp[n-1][1][1][8][8]<<endl;

	return 0;

}