【LeetCode二叉树#04】判断对称二叉树、相同的树、另一棵子树、树的子结构（二叉树相等判断）

对称二叉树

力扣题目链接(opens new window)

给定一个二叉树，检查它是否是镜像对称的。

思路

本题中，不能单纯去比较左右子节点的是否对称（都有值且不为空）

因为如果按上面那样做的话，到子节点后就肯定是不对称的（对于左半边而言），但整体上看可能还是对称的，仍然满足题意，由此就会出现错误

因此，我们需要比较的是当前左右节点下的外侧和内侧的节点是否对称，如图所示：

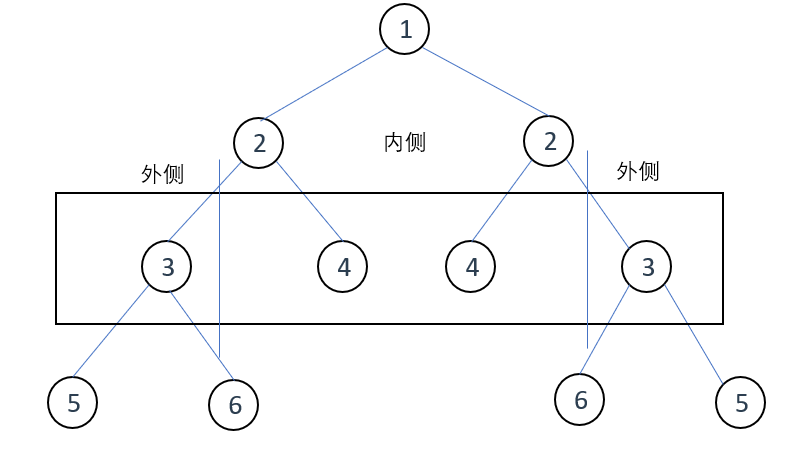
上图中，显然整课二叉树是对称的

我们在判断的时候只需将左2节点与右2节点的子节点按内侧与外侧区分，再进行比较即可

代码

递归法

按照递归三步走来：

1、确定递归函数的参数和返回类型

2、确定递归的终止条件

3、处理下一层的递归逻辑

class Solution {
public:
    //确定递归函数的参数和返回值
    bool cmp(TreeNode* left, TreeNode* right){
        //确定终止条件
        //四种情况
        //空节点情况
        //左节点为空，右节点不为空
        if(left == NULL && right != NULL) return false;
        //左节点不为空，右节点为空
        else if(left != NULL && right == NULL) return false;
        //左节点为空，右节点为空
        else if(left == NULL && right == NULL) return true;

        //非空但值不相等情况
        //左右节点均不为空但值不相等
        else if(left->val != right->val)return false;

        //以下是左右节点均不为空且值相等的情况
        //启用递归去判断他们的子节点（下一层）是否满足对称
        //处理单层逻辑
        bool outside = cmp(left->left, right->right);//外侧
        bool inside = cmp(left->right, right->left);//内侧
        bool res = outside && inside;
        return res;//记得返回最终结果
    }
    bool isSymmetric(TreeNode* root) {
        //判断根节点是否为空
        if(root == NULL) return 0;
        return cmp(root->left, root->right);
    }
};

迭代法

定义两个节点，同时放入 队列 中，然后同时取出判断是否相等，直到遍历结束

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        //创建队列
        queue<TreeNode*> que;
        //判断根节点是否为空，为空直接对称
        if (root == NULL) return true;
        //获取左右节点（相对于root来说的）
        //加入队列
        que.push(root->left);
        que.push(root->right);

        //队列不为空则遍历
        while(!que.empty()){
            //取出队列中的两个节点
            TreeNode* left = que.front();
            que.pop();
            TreeNode* right = que.front();
            que.pop();
            // //左节点为空，右节点有值//左节点有值，右节点为空//左右节点有值但不同
            // if(left == NULL && right != NULL || left != NULL && right == NULL || left->val != right->val){
            //     return false;
            // }else if(left == NULL && right == NULL){
            //     continue;
            // }
            //左右节点均为空
            if(left == NULL && right == NULL){
                continue;
            }

            //队列中如果没有同时放入两个节点就直接代表不对称了，即有一个为空就可以下判断
            //其实还是对应之前的三种情况，只是在队列中表现方式不同
            if((right == NULL || left == NULL|| (left->val != right->val))){
                return false;
            }
            //排除上面的情况后就剩下不为空且对称的情况

            //继续加入当前左右节点的子节点,依旧遵循内外侧原则
            //外侧
            que.push(left->left);
            que.push(right->right);
            //内侧
            que.push(left->right);
            que.push(right->left);
        }
        //完成上述遍历没返回false就是对称的
        return true;
    }
};

注意点

1、因为已经使用了队列，每次我们都需要放入两个节点，如果某次发现取的时候只有一个，那直接就可以判定当前情况为不对称‘

相同的树

https://leetcode.cn/problems/same-tree/

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]

输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]

输出：false

示例 3：

输入：p = [1,2,1], q = [1,1,2]

输出：false

思路

与对称二叉树的解法类似

只不过这里递归函数中，我们输入的分别是两个树的root

在处理单层逻辑时，要遵循以下原则：

二叉树A的左侧节点与二叉树B的左侧节点比较；

二叉树A的右侧节点与二叉树B的右侧节点比较；

上述结果完全相同才能证明两树相同

代码

使用递归法的思路

class Solution {
public:
    //确定递归函数参数与返回值
    bool cmp(TreeNode* p, TreeNode* q){
        //确定终止条件(当前遍历节点为空)
        if(p == NULL && q == NULL) return true;
        else if(p == NULL || q == NULL)return false;
        else if(p->val != q->val)return false;
        //处理单层逻辑
        bool leftside = cmp(p->left, q->left);
        bool rightside = cmp(p->right, q->right);
        bool res = leftside && rightside;
        return res;
    }
    bool isSameTree(TreeNode* p, TreeNode* q) {
        return cmp(q,p);
    }
};

另一颗子树

https://leetcode.cn/problems/subtree-of-another-tree/

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

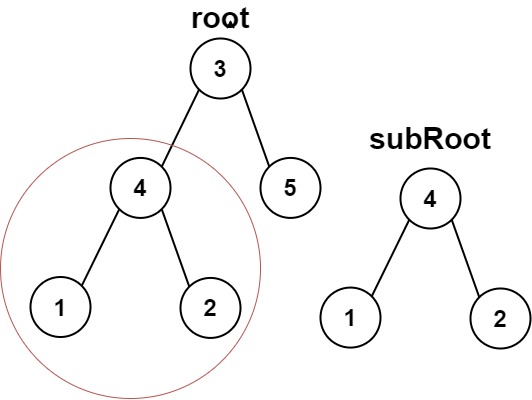
输入：root = [3,4,5,1,2], subRoot = [4,1,2]

输出：true

示例 2：

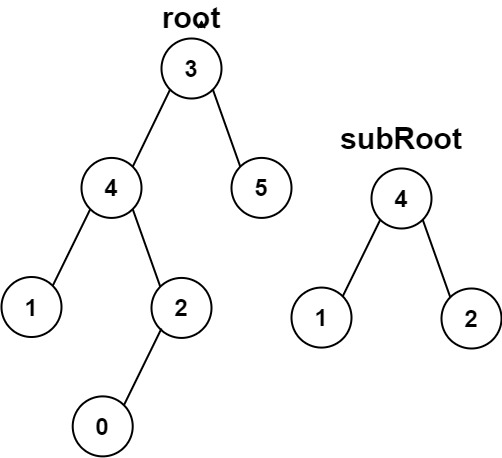
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]

输出：false

提示：

root 树上的节点数量范围是 [1, 2000]

subRoot 树上的节点数量范围是 [1, 1000]

-104 <= root.val <= 104

-104 <= subRoot.val <= 104

思路

先读懂题目，题目要求我们在root中寻找一个与subRoot相等的子树，如果存在该子树返回true，否则返回false

那么会有以下几种情况：

1、root与subRoot直接就是相等的

• 两者都为NULL
• 两者满足相等条件

2、subRoot是root的左子树

3、subRoot是root的右子树

分别针对上述情况进行处理即可

两颗二叉树怎么才算相等？

两颗二叉树相等的定义是它们的结构相同且对应节点的值也相同。

具体来说，以下条件满足时，两颗二叉树才算相等：

1. 两棵树的根节点的值相等。
2. 递归比较两棵树的左子树和右子树是否相等。如果都相等，则这两棵树相等；如果至少有一棵子树不相等，则这两棵树不相等。

需要注意的是，如果一棵树的节点为空，而另一棵树对应节点不为空，则这两棵树不相等。

代码

主函数

一般来说，如果涉及递归操作，都应该先讲递归函数

但是这里有点特殊，我想先说一下主函数（不然会不清楚递归函数要达到的目的）

class Solution {
public:
    //先得有一个用于判断相等数的函数
    //确定递归函数参数与返回值
    bool traversal(TreeNode* p, TreeNode* q){

    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        //root不能为空
        if(root == NULL) return false;

        //root与subRoot相同，true
        // if(traversal(root, subRoot))return true;
        if(root->val == subRoot->val && traversal(root, subRoot)) return true;

        //分别判断root的左边和右边有无与subRoot相同的,满足一边即可
        // return isSameTree(root->left, subRoot) || isSameTree(root->right, subRoot);
        return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

在主函数isSubtree中，我们要判断的root中是否存在subRoot

首先得确定root的根节点不为空

然后判断当前节点（根节点）的值是否与subRoot当前节点的值相等【两棵树的根节点的值相等】

除此之外，还要判断root中是否存在与subRoot相等的子树【结构上相等】

判断结构的时候就需要使用递归函数遍历所有节点了，待会讲递归函数

如果在结构和数值上都相等，那么可以返回true

否则需要在再继续去root的左右子树中找与subRoot相等的子树

具体到操作上就是：递归调用主函数

是的，就是因为这个迷惑的操作，所以需要先说主函数逻辑。。。

在递归查找root左右子树时，只要有一边找到与subRoot相等的子树，主函数就可以返回true

递归函数

根据上述分析，整体代码中其实使用了两处递归

主函数递归负责在root中递归查找左右子树；

而traversal则负责在主函数递归中，判断当前root的子树是否与subRoot相等；

class Solution {
public:
    //先得有一个用于判断相等数的函数
    //确定递归函数参数与返回值
    bool traversal(TreeNode* p, TreeNode* q){
        //确定终止条件(当前遍历节点为空)
        if(p == NULL && q == NULL) return true;//当前root子树和subRoot均为空的情况，相等
        else if(p == NULL || q == NULL) return false;//当前root子树和subRoot一方为空的情况，不相等
        else if(p->val != q->val) return false;//当前root子树和subRoot值不相等，不相等

        //处理单层逻辑
        //递归查找当前root子树的左子树
        bool leftside = traversal(p->left, q->left);
        //递归查找当前root子树的右子树
        bool rightside = traversal(p->right, q->right);
        //综合左右子树情况，均返回true则表示结构上相等，判定当前root子树和subRoot相等
        bool res = leftside && rightside;
        return res;
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {

    }
};

完整代码

class Solution {
public:
    //先得有一个用于判断相等数的函数
    //确定递归函数参数与返回值
    bool traversal(TreeNode* p, TreeNode* q){
        //确定终止条件(当前遍历节点为空)
        if(p == NULL && q == NULL) return true;//当前root子树和subRoot均为空的情况，相等
        else if(p == NULL || q == NULL) return false;//当前root子树和subRoot一方为空的情况，不相等
        else if(p->val != q->val) return false;//当前root子树和subRoot值不相等，不相等

        //处理单层逻辑
        //递归查找当前root子树的左子树
        bool leftside = traversal(p->left, q->left);
        //递归查找当前root子树的右子树
        bool rightside = traversal(p->right, q->right);
        //综合左右子树情况，均返回true则表示结构上相等，判定当前root子树和subRoot相等
        bool res = leftside && rightside;
        return res;
    }

    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        //root不能为空
        if(root == NULL) return false;

        //root与subRoot相同，true
        // if(traversal(root, subRoot))return true;
        if(root->val == subRoot->val && traversal(root, subRoot)) return true;

        //分别判断root的左边和右边有无与subRoot相同的,满足一边即可
        // return isSameTree(root->left, subRoot) || isSameTree(root->right, subRoot);
        return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

树的子结构

https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof/

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:

给定的树 A:

 3
/ \

4 5

/

1 2

给定的树 B：

4

/

1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]

输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]

输出：true

限制：

0 <= 节点个数 <= 10000

思路

与上一题思路一致

代码

代码方面，递归函数的停止条件需要做一下变化

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
private:
    bool traversal(TreeNode* A, TreeNode* B){
        //确定停止条件
        if(B == NULL) return true;//当B遍历到了叶子节点，意味着B树是A树的子结构
        //A、B同时为空表示没找到相同子结构，A先为空则表示B不可能为子结构，均返回false
        if(A == NULL && B == NULL || A == NULL) return false;
        if(A->val != B->val) return false;
        // if(A == NULL || A->val != B->val) return false;//也可以这样判断

        //确定单层处理逻辑
        bool leftside = traversal(A->left, B->left);
        bool rightside = traversal(A->right, B->right);
        bool res = leftside && rightside;
        return res;
    }
public:
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(A == NULL || B == NULL) return false;
        if(A->val == B->val && traversal(A, B)) return true;//确保结构一致

        return isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
};