神经网络优化篇：详解梯度消失/梯度爆炸（Vanishing / Exploding gradients）

梯度消失/梯度爆炸

训练神经网络，尤其是深度神经所面临的一个问题就是梯度消失或梯度爆炸，也就是训练神经网络的时候，导数或坡度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度。

接下来，将会了解梯度消失或梯度爆炸的真正含义，以及如何更明智地选择随机初始化权重，从而避免这个问题。

假设正在训练这样一个极深的神经网络，画的神经网络每层只有两个隐藏单元，但它可能含有更多，但这个神经网络会有参数\(W^{[1]}\)，\(W^{[2]}\)，\(W^{[3]}\)等等，直到\(W^{[l]}\)，为了简单起见，假设使用激活函数\(g(z)=z\)，也就是线性激活函数，忽略\(b\)，假设\(b^{[l]}\)=0，如果那样的话，输出\(y=W^{[l]}W^{[L -1]}W^{[L - 2]} \ldots W^{[3]}W^{[2]}W^{[1]}x\)，如果想考验的数学水平，\(W^{[1]} x = z^{[1]}\)，因为\(b=0\)，所以想\(z^{[1]} =W^{[1]} x\)，\(a^{[1]} = g(z^{[1]})\)，因为使用了一个线性激活函数，它等于\(z^{[1]}\)，所以第一项\(W^{[1]} x = a^{[1]}\)，通过推理，会得出\(W^{[2]}W^{[1]}x =a^{[2]}\)，因为\(a^{[2]} = g(z^{[2]})\)，还等于\(g(W^{[2]}a^{[1]})\)，可以用\(W^{[1]}x\)替换\(a^{[1]}\)，所以这一项就等于\(a^{[2]}\)，这个就是\(a^{[3]}\)(\(W^{[3]}W^{[2]}W^{[1]}x\))。

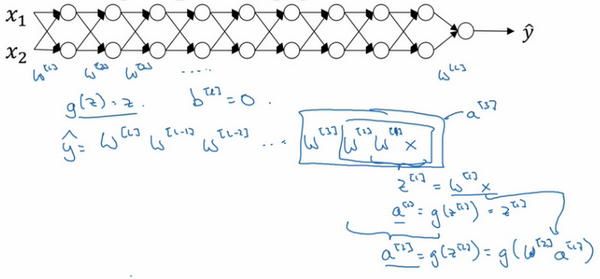
所有这些矩阵数据传递的协议将给出\(\hat y\)而不是\(y\)的值。

假设每个权重矩阵\(W^{[l]} = \begin{bmatrix} 1.5 & 0 \\0 & 1.5 \\\end{bmatrix}\)，从技术上来讲，最后一项有不同维度，可能它就是余下的权重矩阵，\(y= W^{[1]}\begin{bmatrix} 1.5 & 0 \\ 0 & 1.5 \\\end{bmatrix}^{(L -1)}x\)，因为假设所有矩阵都等于它，它是1.5倍的单位矩阵，最后的计算结果就是\(\hat{y}\)，\(\hat{y}\)也就是等于\({1.5}^{(L-1)}x\)。如果对于一个深度神经网络来说\(L\)值较大，那么\(\hat{y}\)的值也会非常大，实际上它呈指数级增长的，它增长的比率是\({1.5}^{L}\)，因此对于一个深度神经网络，\(y\)的值将爆炸式增长。

相反的，如果权重是0.5，\(W^{[l]} = \begin{bmatrix} 0.5& 0 \\ 0 & 0.5 \\ \end{bmatrix}\)，它比1小，这项也就变成了\({0.5}^{L}\)，矩阵\(y= W^{[1]}\begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \\\end{bmatrix}^{(L - 1)}x\)，再次忽略\(W^{[L]}\)，因此每个矩阵都小于1，假设\(x_{1}\)和\(x_{2}\)都是1，激活函数将变成\(\frac{1}{2}\)，\(\frac{1}{2}\)，\(\frac{1}{4}\)，\(\frac{1}{4}\)，\(\frac{1}{8}\)，\(\frac{1}{8}\)等，直到最后一项变成\(\frac{1}{2^{L}}\)，所以作为自定义函数，激活函数的值将以指数级下降，它是与网络层数数量\(L\)相关的函数，在深度网络中，激活函数以指数级递减。

希望得到的直观理解是，权重\(W\)只比1略大一点，或者说只是比单位矩阵大一点，深度神经网络的激活函数将爆炸式增长，如果\(W\)比1略小一点，可能是\(\begin{bmatrix}0.9 & 0 \\ 0 & 0.9 \\ \end{bmatrix}\)。

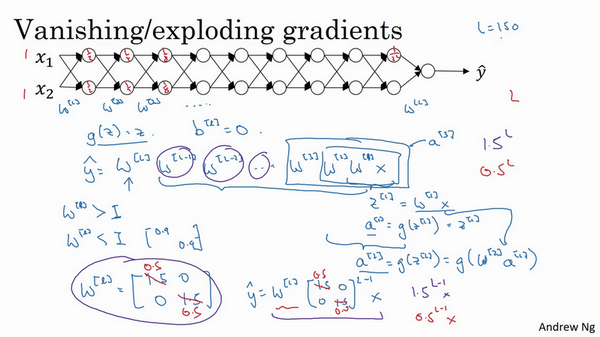
在深度神经网络中，激活函数将以指数级递减，虽然只是讨论了激活函数以与\(L\)相关的指数级数增长或下降，它也适用于与层数\(L\)相关的导数或梯度函数，也是呈指数级增长或呈指数递减。

对于当前的神经网络，假设\(L=150\)，最近Microsoft对152层神经网络的研究取得了很大进展，在这样一个深度神经网络中，如果激活函数或梯度函数以与\(L\)相关的指数增长或递减，它们的值将会变得极大或极小，从而导致训练难度上升，尤其是梯度指数小于\(L\)时，梯度下降算法的步长会非常非常小，梯度下降算法将花费很长时间来学习。

总结一下，讲了深度神经网络是如何产生梯度消失或爆炸问题的，实际上，在很长一段时间内，它曾是训练深度神经网络的阻力，虽然有一个不能彻底解决此问题的解决方案，但是已在如何选择初始化权重问题上提供了很多帮助。