2022-02-06：等差数列划分 II - 子序列。 给你一个整数数组 nums ，返回 nums 中所有 等差子序列 的数目。 如果一个序列中 至少有三个元素 ，并且任意两个相邻元素之差相同，则称

2022-02-06：等差数列划分 II - 子序列。
给你一个整数数组 nums ，返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该序列为等差序列。
例如，[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。
再例如，[1, 1, 2, 5, 7] 不是等差序列。
数组中的子序列是从数组中删除一些元素（也可能不删除）得到的一个序列。
例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
题目数据保证答案是一个 32-bit 整数。
示例 1：
输入：nums = [2,4,6,8,10]
输出：7
解释：所有的等差子序列为：
[2,4,6]
[4,6,8]
[6,8,10]
[2,4,6,8]
[4,6,8,10]
[2,4,6,8,10]
[2,6,10]
提示：
1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
力扣446。

答案2022-02-06：

dp[i]是一个map，i一定要做结尾。键是差值，值是个数。
时间复杂度：O( (logN) 平方)。
时间复杂度：O( (logN) 平方)。

代码用golang编写。代码如下：

import (
    "fmt"
    "math"
)

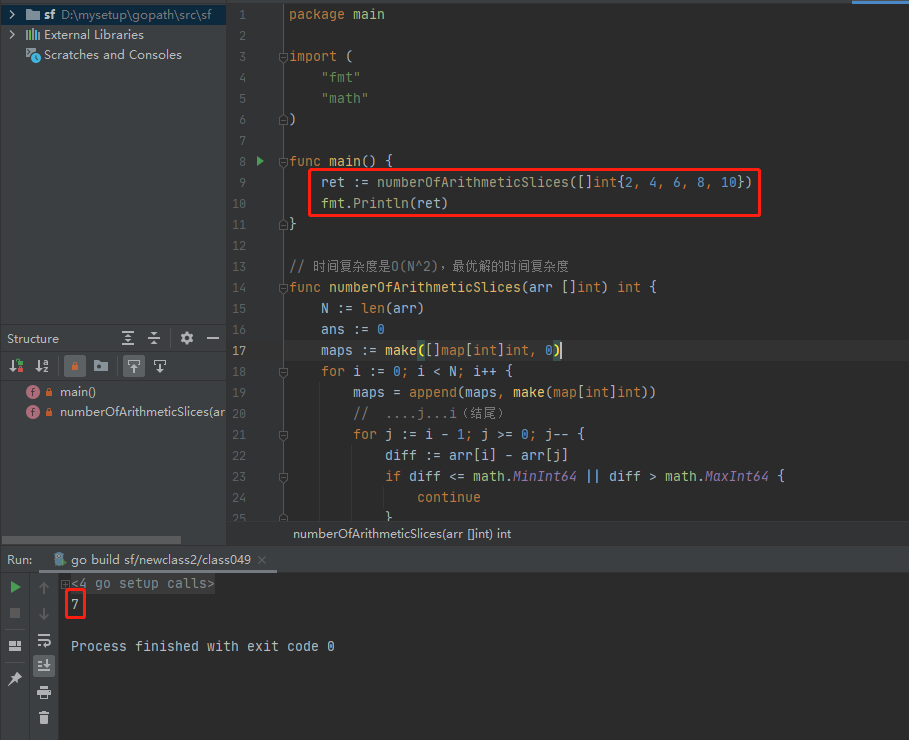
func main() {
    ret := numberOfArithmeticSlices([]int{2, 4, 6, 8, 10})
    fmt.Println(ret)
}

// 时间复杂度是O(N^2)，最优解的时间复杂度
func numberOfArithmeticSlices(arr []int) int {
    N := len(arr)
    ans := 0
    maps := make([]map[int]int, 0)
    for i := 0; i < N; i++ {
        maps = append(maps, make(map[int]int))
        //  ....j...i（结尾）
        for j := i - 1; j >= 0; j-- {
            diff := arr[i] - arr[j]
            if diff <= math.MinInt64 || diff > math.MaxInt64 {
                continue
            }
            dif := diff
            count := maps[j][dif]
            ans += count
            maps[i][dif] += count + 1
        }
    }
    return ans
}

执行结果如下：

---

左神java代码