DP Record

从 2024/5/4 往后开始记录捏。

T1.

给你一棵树，定义一个集合的权值为 \(\dfrac{\sum_{x\in S}V_x}{\sum_{x\in S}C_x}\)。若一个点 \(\in S\)，则其父亲也必须 \(\in S\) 并且 \(|S| = k\)。求满足条件的所有集合的最大价值。\(n,k \le 2500\)。

Solution:

注意到那一个奇妙的式子和这个奇妙的条件，我们可以联想到 \(0/1\) 分数规划。不会的出门右转。

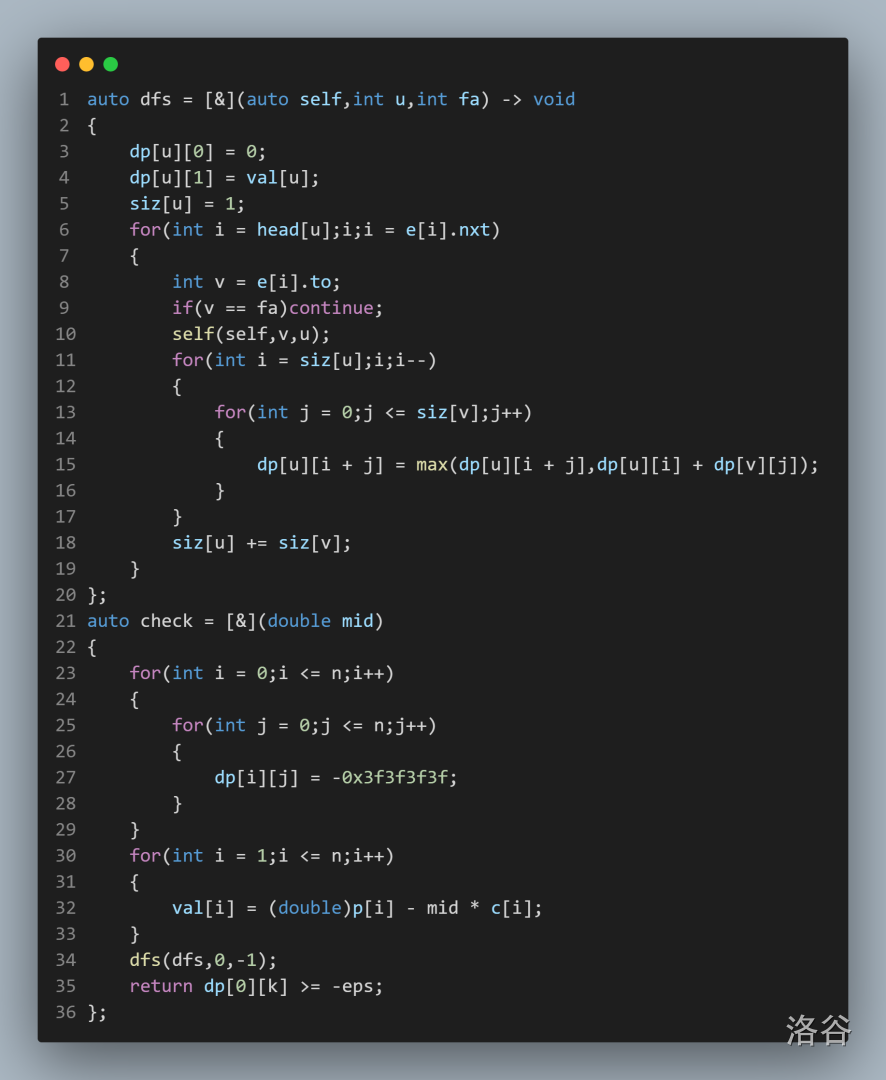
我们定义 \(dp_{u,s}\) 为在 \(u\) 的子树下我们一共选择了整整 \(s\) 个点。

所以我们可以对于每一个儿子节点都举出他的子树中选择了多少个点然后对于所有情况取个 \(\max\) 即可的到 \(dp_{u,s}\)。然后我们在进行 \(0/1\) 分规即可。

T2.Sam数

我们定义 \(dp_{i,j}\) 为第 \(i\) 为是 \(j\) 的方案数。于是我们可以非常迅速的得到递推式，\(dp_{i,x} = \sum^{j + 2}_{x = j - 2} dp_{i - 1,x}\)。

但是这个算法的复杂度明显为 \(O(n)\)，可以得到 \(30\) 分的高分。但是对于 \(n \le 10^{18}\)，我们需要 \(O(\log n)\) 的写法。

对于这个式子，我们可以考虑使用矩阵快速幂进行优化。

矩阵非常好推，自己写。

T3.P3412

较为综合的好题。

我们发现题目等价于把 \(a\) 作为根，然后其余的节点到 \(a\) 的期望值之和。然后我们可以枚举每一个 \(a\) 进行计算。

我们定义 \(dp_u\) 为 \(u\) 子树内其所有的点到 \(u\) 的期望步数。如果这个点的所有子树都聚集到了这个点上，但是我们无法计算出这个点去到其父亲的期望步数。

于是我们再定义 \(g_u\) 为 \(u\) 节点到其父亲的期望步数。

然后我们考虑如何转移 \(g_u\)。

1. \(u\) 直接走到了他的父亲。

2. 他往下走了。

则有 \(g_u = \dfrac{1}{deg_u} + \sum_{v \in son_u} \dfrac{g_v + g_u + 1}{deg_u}\)。

所以 \(g_u \times deg_u = 1 + \sum_{v \in son_u}(g_v + g_u + 1) = deg_u + (deg_u - 1) \times g_u + \sum_{v \in son_u}g_v\)。

于是 \(g_u = deg_u + \sum_{v \in son_u}g_v\)。

然后我们来计算 \(dp_u\)。\(dp_u = \sum_{v \in son_u}dp_v + g_v \times siz_v\)，这是显而易见的。

时间复杂度为 \(O(n^2)\)。

由于每一个节点均有可能作为根节点，所以我们考虑换根 \(dp\)。

假设 \(h_u\) 为以 \(u\) 为根节点，其他节点到这个点的期望步数之和。显然的答案为 \(\dfrac{\sum_{u = 1}^{u \le n} h_u}{n^2}\)。

按照正常的换根 \(dp\) 的转移方式转移即可。

所以可以得出 \(h_u = dp_u + h_{fa_u} - dp_u - siz_u \times g_u + (n - siz_u) \times (g_1 - g_n)\)。

特殊的 \(h_1 = f_1\)。

这样子我们就可以将这个题的复杂度化为 \(O(n)\) 了。