什么是B-Tree

　　B-Tree就是我们常说的B树，一定不要读成B减树，否则就很丢人了。B树这种数据结构常常用于实现数据库索引，因为它的查找效率比较高。

B-Tree与二叉查找树的对比

　　我们知道二叉查找树查询的时间复杂度是O（logN），查找速度最快和比较次数最少，既然性能已经如此优秀，但为什么实现索引是使用B-Tree而不是二叉查找树，关键因素是磁盘IO的次数。

数据库索引是存储在磁盘上，当表中的数据量比较大时，索引的大小也跟着增长，达到几个G甚至更多。当我们利用索引进行查询的时候，不可能把索引全部加载到内存中，只能逐一加载每个磁盘页，这里的磁盘页就对应索引树的节点。

一、 二叉树

我们先来看二叉树查找时磁盘IO的次：定义一个树高为4的二叉树，查找值为10：

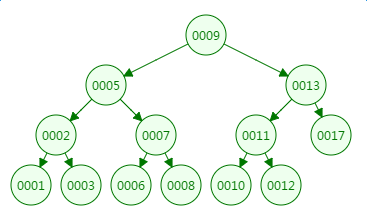
第一次磁盘IO：

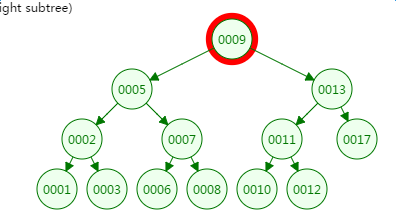
第二次磁盘IO

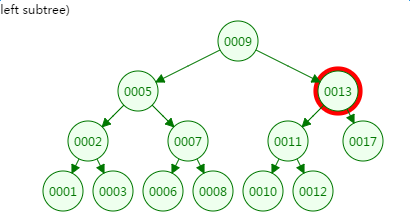
第三次磁盘IO:

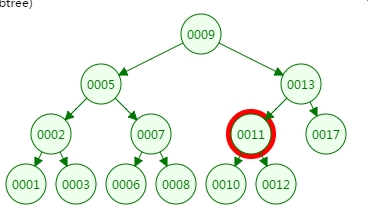
第四次磁盘IO：

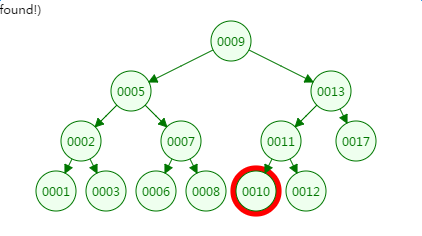
从二叉树的查找过程了来看，树的高度和磁盘IO的次数都是4，所以最坏的情况下磁盘IO的次数由树的高度来决定。

从前面分析情况来看，减少磁盘IO的次数就必须要压缩树的高度，让瘦高的树尽量变成矮胖的树，所以B-Tree就在这样伟大的时代背景下诞生了。

二、B-Tree

m阶B-Tree满足以下条件：

1、每个节点最多拥有m个子树

2、根节点至少有2个子树

3、分支节点至少拥有m/2颗子树（除根节点和叶子节点外都是分支节点）

4、所有叶子节点都在同一层、每个节点最多可以有m-1个key，并且以升序排列

如下有一个3阶的B树，观察查找元素21的过程：

第一次磁盘IO：

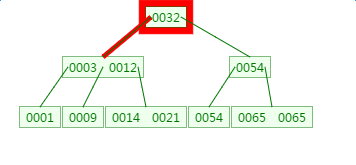
第二次磁盘IO：

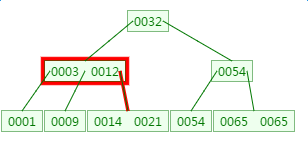
这里有一次内存比对：分别跟3与12比对

第三次磁盘IO:

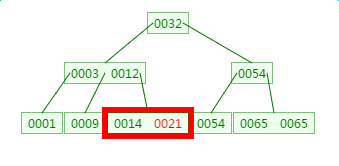
这里有一次内存比对，分别跟14与21比对

从查找过程中发现，B树的比对次数和磁盘IO的次数与二叉树相差不了多少，所以这样看来并没有什么优势。

但是仔细一看会发现，比对是在内存中完成中，不涉及到磁盘IO，耗时可以忽略不计。另外B树种一个节点中可以存放很多的key（个数由树阶决定）。

相同数量的key在B树中生成的节点要远远少于二叉树中的节点，相差的节点数量就等同于磁盘IO的次数。这样到达一定数量后，性能的差异就显现出来了。

三、B树的新增

在刚才的基础上新增元素4，它应该在3与9之间：

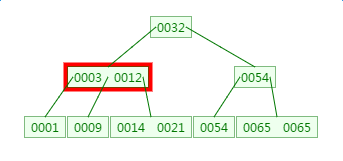
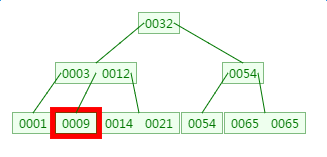
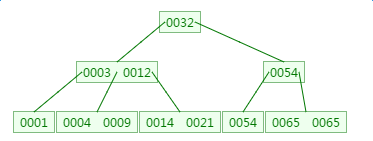
四、B树的删除

删除元素9：

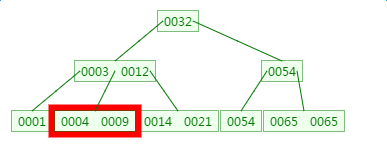
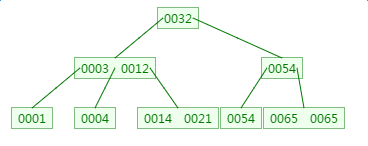
五、总结

　　插入或者删除元素都会导致节点发生裂变反应，有时候会非常麻烦，但正因为如此才让B树能够始终保持多路平衡，这也是B树自身的一个优势：自平衡；B树主要应用于文件系统以及部分数据库索引，如MongoDB，大部分关系型数据库索引则是使用B+树实现。