UVa 11168 (凸包+点到直线距离) Airport

题意：

平面上有n个点，求一条直线使得所有点都在直线的同一侧。并求这些点到直线的距离之和的最小值。

分析：

只要直线不穿过凸包，就满足第一个条件。要使距离和最小，那直线一定在凸包的边上。所以求出凸包以后，枚举每个边求出所有点到直线的距离之和得到最小值。

点到直线距离公式为：

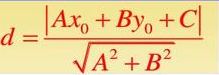
因为点都在直线同一侧，所以我们可以把加法“挪”到里面去，最后再求绝对值，所以可以预处理所有点的横坐标之和与纵坐标之和。当然常数C也要记得乘上n倍。

已知两点坐标求过该点直线的方程，这很好求不再赘述，考虑到直线没有斜率的情况，最终要把表达式中的分母乘过去。

 //#define LOCAL
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 #include <vector>
 using namespace std;

 struct Point
 {
     double x, y;
     Point(double x=, double y=):x(x), y(y) {}
 };
 typedef Point Vector;
 Point operator + (Point A, Point B)
 {
     return Point(A.x+B.x, A.y+B.y);
 }
 Point operator - (Point A, Point B)
 {
     return Point(A.x-B.x, A.y-B.y);
 }
 bool operator < (const Point& A, const Point& B)
 {
     return A.x < B.x || (A.x == B.x && A.y < B.y);
 }
 bool operator == (const Point& A, const Point& B)
 {
     return A.x == B.x && A.y == B.y;
 }
 double Cross(Vector A, Vector B)
 {
     return A.x*B.y - A.y*B.x;
 }

 vector<Point> ConvexHull(vector<Point> p) {
   // 预处理，删除重复点
   sort(p.begin(), p.end());
   p.erase(unique(p.begin(), p.end()), p.end());

   int n = p.size();
   int m = ;
   vector<Point> ch(n+);
   for(int i = ; i < n; i++) {
     while(m >  && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
     ch[m++] = p[i];
   }
   int k = m;
   for(int i = n-; i >= ; i--) {
     while(m > k && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
     ch[m++] = p[i];
   }
   if(n > ) m--;
   //for(int i = 0; i < m; ++i) printf("%lf %lf\n", ch[i].x, ch[i].y);
   ch.resize(m);
   return ch;
 }

 double sumx, sumy;

 double Dist(Point a, Point b, int m)
 {
     double A = a.y-b.y, B = b.x-a.x, C = a.x*b.y - b.x*a.y;
     //printf("%lf %lf", fabs(A*sumx+B*sumy+C), sqrt(A*A+B*B));
     return (fabs(A*sumx+B*sumy+C*m) / sqrt(A*A+B*B));
 }

 int main(void)
 {
     #ifdef LOCAL
         freopen("11168in.txt", "r", stdin);
     #endif

     int T;
     scanf("%d", &T);
     for(int kase = ; kase <= T; ++kase)
     {
         int n;
         vector<Point> p;
         sumx = 0.0, sumy = 0.0;
         scanf("%d", &n);
         for(int i = ; i < n; ++i)
         {
             double x, y;
             scanf("%lf%lf", &x, &y);
             p.push_back(Point(x, y));
             sumx += x;    sumy += y;
         }
         vector<Point> ch = ConvexHull(p);
         int m = ch.size();
         //for(int i = 0; i < m; ++i)    printf("%lf %lf\n", ch[i].x, ch[i].y);
         if(m <= )
         {
             printf("Case #%d: 0.000\n", kase);
             continue;
         }

         double ans = 1e10;
         for(int i = ; i < m; ++i)
             ans = min(ans, Dist(ch[i], ch[(i+)%m], n));
         printf("Case #%d: %.3lf\n", kase, ans/n);
     }
 }

代码君