jmeter后置处理器之正则表达式

一、基本用法——提取某个值

场景：提取某个值，保存成变量，供后面的接口使用

步骤：

1、运行脚本，从响应结果中查找要提取的值，找到左右边界。

例如要获取“patientInfoId”作为下一个请求的参数，"patientInfoId":"2c92e0e66680b7da0166820bcb7301a1".

2、添加后置处理器——正则表达式提取器

• 1、引用名称：就是变量名，调用使用${patientInfoId}
• 2、正则表达式：()括号里表示你要的数值，相当于LR的右边界
• 3、模板：$$表示你要是用那个正则表达式那个模板获取的值   -1全部，0 随机，1第一个2第二个，如果只有一个正则一般就填写1，如果多个正则你要看你到底调用哪个值来定，这儿待会下面截图例子一看就明白
• 4、匹配数字：-1表示全部，0随机，1第一个，2第二个
• 5、缺省值：这个如果没有匹配到，给它定义的一个默认值
• 6、注意事项：正则表达式中的特殊字符需要转义\

3、引用参数

二、升级用法——提取多个值

需求：提取医生排班的营业时间段的起止时间

步骤（方案一）：

1、查找响应中的目标值

2、添加正则表达式提取器，设置如下

有三种设置方式，分别如下：

区别是period的值不同

• 第一种

period=19:0023:00
period_g=2
period_g0="periodStart":"19:00","periodEnd":"23:00"
period_g1=19:00
period_g2=23:00

• 第二种

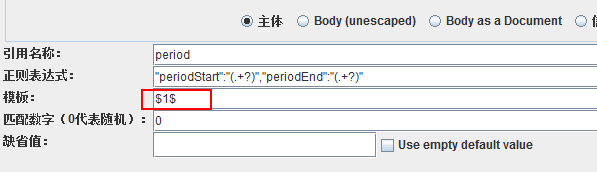
period=19:00
period_g=2
period_g0="periodStart":"19:00","periodEnd":"23:00"
period_g1=19:00
period_g2=23:00

• 第三种

period=23:00
period_g=2
period_g0="periodStart":"19:00","periodEnd":"23:00"
period_g1=19:00
period_g2=23:00

3、引用参数

${period_g1}

${period_g2}

三、升级用法——提取一组值

需求：查看所有家庭成员，返回所有的patientId（一组），并对每个patientId进行挂号操作（循环遍历）。

步骤1、同上

步骤2、添加正则表达式提取器

正则表达式提取器设置如下：

步骤3、引用参数

参数引用如下：

步骤4、使用ForEach控制器，实现遍历

添加ForEach控制器，配置如下

注意：

• 输入变量前缀：输入正则表达式变量的引用名称即可
• Start index for loop(exclusive) 指定目标值的开始索引(不包含填写值)，默认为0
• End index for loop(exclusive) 指定目标值的结束索引(包含填写值)，默认最大索引值。

　　　　如果要遍历分组中的全部遍历，Start index for loop(exclusive),End index for loop(exclusive)默认为空即可。

• Add “_” before number? 默认勾选状态，根据填写值来决定是否勾选，如下,如果输入变量前缀填写引用名称_则可以不勾选，否则必须勾选

• 输出变量名称：用于存储每次遍历获取值，供其它地方引用

步骤5、

参数引用：使用${patientId}