点权生成树(gentree)

点权生成树(gentree)

题目背景

Awson是某国际学校信竞组的一只菜鸡。终于弄明白边权最小生成树后，然而又被大神嘲笑了。大神深邃的眼光中透露了些睿智，说道：“你会求点权最小生成树么？”Awson不屑的说道：“不会。但我有办法。”于是他找到了你，请你帮他解决这个问题。

题目描述

给你一个有向连通图G，每点有个权值Di（0<Di），要求生成一棵树根为1号节点的有根树T。对于树中边E，E的代价为所有从根出发的且包含E的路径的终点权值的和。现求生成树T，使得边的代价总和最小。

输入输出格式

输入格式：

第一行N,M分别为点数，边数。（0<=N <= 20000；0<=M <= 200000）

接下来M行，每行两个数U，V描述边的两个端点，即从U到V有一条有向边。

最后一行N个数，顺次给出每个点的权值。

输出格式：

一个数，最小代价。

输入输出样例

输入样例#1：

5 4
1 2
1 3
3 4
3 5
1 2 3 4 5

输出样例#1：

23

说明

样例解释：

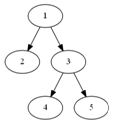
如图只有一种生成树的方法，求得代价为23。

数据规模：

所有数据保证不会超过长整型（C++中的int）。

题解：

归纳发现，算出的总代价就是每个节点在生成树中的深度×点权的和。

我们用贪心的思想，每个点的深度都要尽可能小。那么我们只需以1号节点为源点，跑一遍最短路即可。

由最小生成树的思想，我们易知所有求出的最短路径都在一棵生成树上，满足题意。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
using namespace std;
int n,m,ans,a[];
int head[],size=;
struct node
{
    int to,next;
}edge[];
void putin(int from,int to)
{
    size++;
    edge[size].to=to;
    edge[size].next=head[from];
    head[from]=size;
}
int dist[];
bool vis[];
void spfa(int r)
{
    int i,j;
    memset(dist,/,sizeof(dist));
    queue<int>mem;
    while(!mem.empty())mem.pop();
    mem.push(r);
    vis[r]=;
    dist[r]=;
    while(!mem.empty())
    {
        int x=mem.front();mem.pop();
        vis[x]=;
        for(i=head[x];i!=-;i=edge[i].next)
        {
            int y=edge[i].to;
            if(dist[y]>dist[x]+)
            {
                dist[y]=dist[x]+;
                if(!vis[y])
                {
                    mem.push(y);
                    vis[y]=;
                }
            }
        }
    }
}
int main()
{
    int i,j;
    memset(head,-,sizeof(head));
    scanf("%d%d",&n,&m);
    for(i=;i<=m;i++)
    {
        int from,to;
        scanf("%d%d",&from,&to);
        putin(from,to);
    }
    for(i=;i<=n;i++)
    scanf("%d",&a[i]);
    spfa();
    for(i=;i<=n;i++)
    ans+=a[i]*dist[i];
    printf("%d\n",ans);
    return ;
}