本文由zhangbaochong原创，转载请注明出处http://www.cnblogs.com/zhangbaochong/p/5573970.html

　　前面实现简单地形的教程，我们只是绘制了一个网格，这一次我们来学习一下几种基本几何体的绘制，包括平面网格、立方体、圆柱和球体等。

原来在GeometryGenerator类中只给出了CreateGrid一个方法来绘制网格，现在让我们添加其他方法绘制一些几何体。

　　为了方便绘制几何体方法的调用，GeometryGenerator类我们使用了单例模式。很简单，将构造函数设为private，添加一个GetInstance函数如下:

//单例模式

    static GeometryGenerator* GetInstance()

    {

        static GeometryGenerator instance;

        return &instance;

    }

　　这只是实现单例模式的一种方法，还有几种实现单例模式的方法就不一一说明了。

1.基本几何体绘制方法　

　　下面介绍几种常见几何体的绘制方法(代码均参考dx11龙书)。

1.1网格

　　网格可以说是最常见同时也是最重要的，像实现地形水面等都离不开网格。生成一个网格首先要给出网格的宽和高，以及在宽和高上划分的格子数。

看龙书中给出的一张图片就明白了：

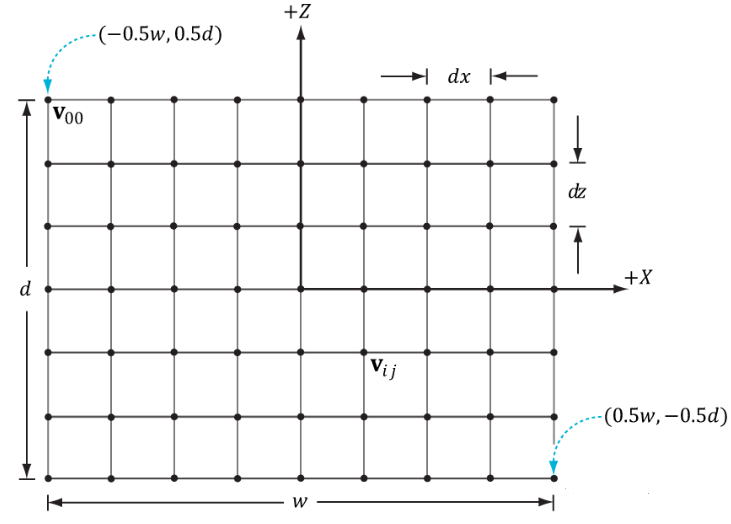
由此，顶点的坐标就很容易生成了。

顶点索引的计算关键是推导出一个用于求构成第i行，第j列的顶点处右下方两个三角形的顶点索引的通用公式。

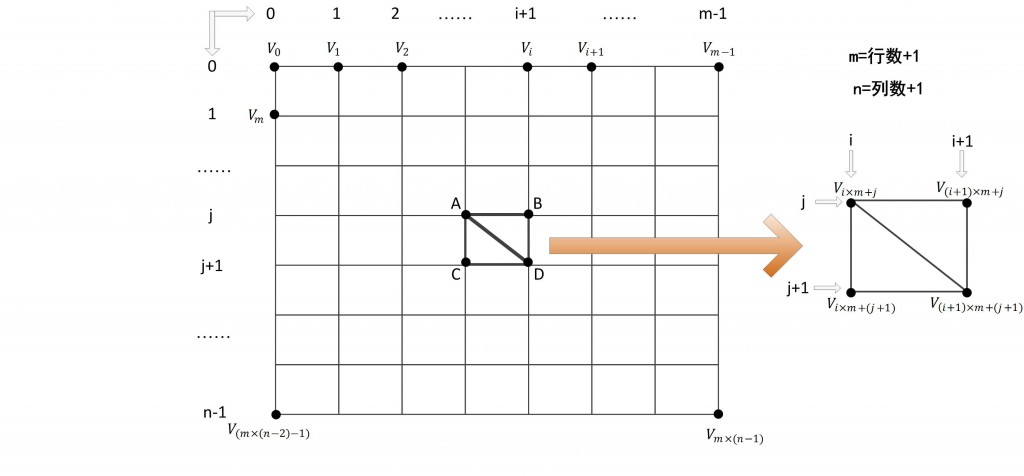
对顶点缓存中的任意一点A，如果该点位于地形中的第i行、第j列的话，那么该点在顶点缓存中所对应的位置应该就是i*m+j（m为每行的顶点数）。如果A点在索引缓存中的位置为k的话，那么A点为起始点构成的三角形ABC中，B、C顶点在顶点缓存中的位置就为（i+1）x m+j和i x m+（j+1）。且B点索引值为k+1，C点索引值为k+2.这样。这样，公式就可以推导为如下：

三角形ABC=【i*每行顶点数+j，i*每行顶点数+（j+1），（i+1）*行顶点数+j】

三角形CBD=【（i+1）*每行顶点数+j，i*每行顶点数+（j+1），（i+1）*行顶点数+（j+1）】

 void GeometryGenerator::CreateGrid(float width, float height, UINT m, UINT n, MeshData &mesh)

 {

     mesh.vertices.clear();

     mesh.indices.clear();

     //每行顶点数、每列顶点数

     UINT nVertsRow = m + ;

     UINT nVertsCol = n + ;

     //起始x、z坐标

     float oX = -width * 0.5f;

     float oZ = height * 0.5f;

     //每一格坐标变化

     float dx = width / m;

     float dz = height / n;

     //顶点总数量：nVertsRow * nVertsCol

     mesh.vertices.resize(nVertsRow * nVertsCol);

     //逐个添加顶点

     for (UINT i = ; i < nVertsCol; ++i)

     {

         float tmpZ = oZ - dz * i;

         for (UINT j = ; j < nVertsRow; ++j)

         {

             UINT index = nVertsRow * i + j;

             mesh.vertices[index].pos.x = oX + dx * j;

             mesh.vertices[index].pos.y = .f;

             mesh.vertices[index].pos.z = tmpZ;

             mesh.vertices[index].normal = XMFLOAT3(.f, .f, .f);

             mesh.vertices[index].tangent = XMFLOAT3(.f, .f, .f);

             mesh.vertices[index].tex = XMFLOAT2(dx*i, dx*j);

         }

     }

     //总格子数量:m * n

     //因此总索引数量: 6 * m * n

     UINT nIndices = m * n * ;

     mesh.indices.resize(nIndices);

     UINT tmp = ;

     for (UINT i = ; i < n; ++i)

     {

         for (UINT j = ; j < m; ++j)

         {

             mesh.indices[tmp] = i * nVertsRow + j;

             mesh.indices[tmp + ] = i * nVertsRow + j + ;

             mesh.indices[tmp + ] = (i + ) * nVertsRow + j;

             mesh.indices[tmp + ] = i * nVertsRow + j + ;

             mesh.indices[tmp + ] = (i + ) * nVertsRow + j + ;

             mesh.indices[tmp + ] = (i + ) * nVertsRow + j;

             tmp += ;

         }

     }

 }

1.2立方体

　　立方体的绘制就很简单了，一个立方体只需要提供三维方向上的长度。有一点与之前绘制彩色立方体时不一样的是，我们这里创建立方体用到24个顶点（每个面4个），而之前彩色立方体只用到了8个顶点（每个顶点被3个面共享）。这是因为在后面学习过程中我们需要顶点的法线坐标，而一个顶点相对于其连接的3个面来说，法线完全不同，因此无法共享顶点。

 void GeometryGenerator::CreateBox(float width, float height, float depth, MeshData &mesh)

 {

     mesh.vertices.clear();

     mesh.indices.clear();

     //一共24个顶点(每面4个)

     mesh.vertices.resize();

     //一共36个索引(每面6个)

     mesh.indices.resize();

     float halfW = width * 0.5f;

     float halfH = height * 0.5f;

     float halfD = depth * 0.5f;

     //眼睛面向z轴正方向

     //构建顶点

     //前面

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //左侧面

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, -.f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //背面

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(-.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //右侧面

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //上面

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //底面

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, -.f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(-halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, -.f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, -halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, -.f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     mesh.vertices[].pos = XMFLOAT3(halfW, -halfH, halfD);

     mesh.vertices[].normal = XMFLOAT3(.f, -.f, .f);

     mesh.vertices[].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[].tex = XMFLOAT2(.f, .f);

     //构建索引

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

     mesh.indices[] = ;

 }

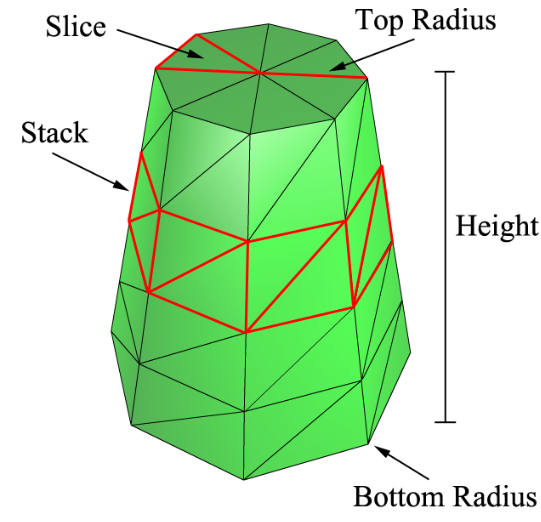
1.3圆柱

　　为了构建一个圆柱，需要提供如下信息：圆柱的上口半径(topRadius)，下口半径(bottomRadius)，高度(height)。此外，为了指定圆柱的精细度，还需要指定两个参数，一个为没高度方向上平均划分的个数(stack)，另一个为沿圆周方向等分的个数(slice)。

　　可以根据龙书中给出的图理解一下：

 void GeometryGenerator::CreateCylinder(float topRadius, float bottomRadius, float height, int slice, int stack, MeshData &mesh)

 {

     mesh.vertices.clear();

     mesh.indices.clear();

     //从上到下每个stack半径变化量:dRadius

     float dRadius = (bottomRadius - topRadius) / stack;

     //每个stack高度:dHeight

     float dHeight = height / stack;

     //每个圆周上顶点数量:slice+1

     int vertsPerRow = slice + ;

     //顶点行数:stack+1

     int nRows = stack + ;

     //总顶点数

     int nVerts = vertsPerRow * nRows;

     //总索引数

     int nIndices = slice * stack * ;

     mesh.vertices.resize(nVerts);

     mesh.indices.resize(nIndices);

     //顶部Y坐标

     float topY = height * 0.5f;

     for (int i = ; i < nRows; ++i)

     {

         float tmpY = topY - dHeight * i;

         float tmpRadius = topRadius + i * dRadius;

         for (int j = ; j < vertsPerRow; ++j)

         {

             float theta = XM_2PI * j / slice;

             int index = i * vertsPerRow + j;

             mesh.vertices[index].pos = XMFLOAT3(tmpRadius*cos(theta), tmpY, tmpRadius*sin(theta));

         }

     }

     UINT tmp();

     for (int i = ; i < stack; ++i)

     {

         for (int j = ; j < slice; ++j)

         {

             mesh.indices[tmp] = i * vertsPerRow + j;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j + ;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j;

             mesh.indices[tmp + ] = i * vertsPerRow + j;

             mesh.indices[tmp + ] = i * vertsPerRow + j + ;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j + ;

             tmp += ;

         }

     }

 }

1.4球

　　绘制球基本参数只有一个半径，但是同圆柱一样为了指定精细程度也要给出stack和slice两个参数，这里slice是从上极点沿球面到下极点的180度角等分。具体绘制可以看代码理解：

 void GeometryGenerator::CreateSphere(float radius, int slice, int stack, MeshData &mesh)

 {

     mesh.vertices.clear();

     mesh.indices.clear();

     int vertsPerRow = slice + ;

     int nRows = stack - ;

     int nVerts = vertsPerRow * nRows + ;

     int nIndices = (nRows - )*slice *  + slice * ;

     mesh.vertices.resize(nVerts);

     mesh.indices.resize(nIndices);

     for (int i = ; i <= nRows; ++i)

     {

         float phy = XM_PI * i / stack;

         float tmpRadius = radius * sin(phy);

         for (int j = ; j < vertsPerRow; ++j)

         {

             float theta = XM_2PI * j / slice;

             UINT index = (i - )*vertsPerRow + j;

             float x = tmpRadius*cos(theta);

             float y = radius*cos(phy);

             float z = tmpRadius*sin(theta);

             //位置坐标

             mesh.vertices[index].pos = XMFLOAT3(x, y, z);

             //法线

             XMVECTOR N = XMVectorSet(x, y, z, .f);

             XMStoreFloat3(&mesh.vertices[index].normal, XMVector3Normalize(N));

             //切线

             XMVECTOR T = XMVectorSet(-sin(theta), .f, cos(theta), .f);

             XMStoreFloat3(&mesh.vertices[index].tangent, XMVector3Normalize(T));

             //纹理坐标

             mesh.vertices[index].tex = XMFLOAT2(j*.f / slice, i*.f / stack);

         }

     }

     int size = vertsPerRow * nRows;

     //添加顶部和底部两个顶点信息

     mesh.vertices[size].pos = XMFLOAT3(.f, radius, .f);

     mesh.vertices[size].normal = XMFLOAT3(.f, .f, .f);

     mesh.vertices[size].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[size].tex = XMFLOAT2(.f, .f);

     mesh.vertices[size + ].pos = XMFLOAT3(.f, -radius, .f);

     mesh.vertices[size + ].normal = XMFLOAT3(.f, -.f, .f);

     mesh.vertices[size + ].tangent = XMFLOAT3(.f, .f, .f);

     mesh.vertices[size + ].tex = XMFLOAT2(.f, .f);

     UINT tmp();

     int start1 = ;

     int start2 = mesh.vertices.size() - vertsPerRow - ;

     int top = size;

     int bottom = size + ;

     for (int i = ; i < slice; ++i)

     {

         mesh.indices[tmp] = top;

         mesh.indices[tmp + ] = start1 + i + ;

         mesh.indices[tmp + ] = start1 + i;

         tmp += ;

     }

     for (int i = ; i < slice; ++i)

     {

         mesh.indices[tmp] = bottom;

         mesh.indices[tmp + ] = start2 + i;

         mesh.indices[tmp + ] = start2 + i + ;

         tmp += ;

     }

     for (int i = ; i < nRows - ; ++i)

     {

         for (int j = ; j < slice; ++j)

         {

             mesh.indices[tmp] = i * vertsPerRow + j;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j + ;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j;

             mesh.indices[tmp + ] = i * vertsPerRow + j;

             mesh.indices[tmp + ] = i * vertsPerRow + j + ;

             mesh.indices[tmp + ] = (i + ) * vertsPerRow + j + ;

             tmp += ;

         }

     }

 }

2.场景绘制

2.1最终效果

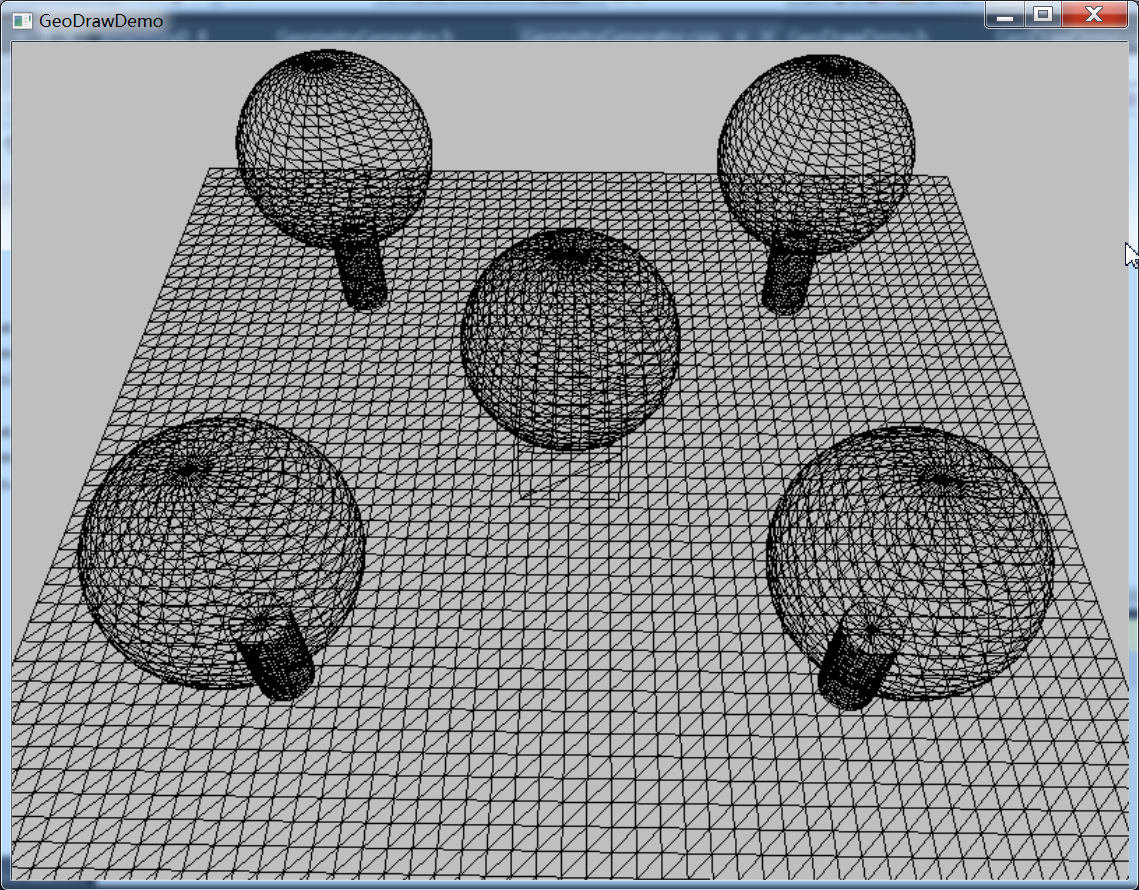
2.2多个几何体共享顶点索引缓冲区

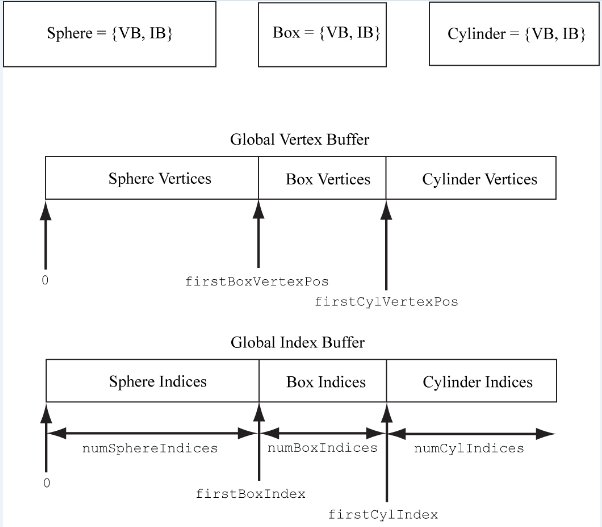
　　我们一共绘制了四种几何体：网格、立方体、球和圆柱，它们公用了一个顶点和索引缓冲区。这样我们就需要在其中找出每个几何体对应的位置。

为了在顶点、索引缓冲区中找到一个物体对应的位置，我们使用三个参数：该物体在顶点缓冲区中的起始位置(VStart),索引缓冲区中的起始位置(IStart)，以及索引总数(totalIndices)。看龙书中的一幅图就很容易理解了：

2.3设为线框模式绘制

　　在Render函数中创建一个栅格化状态ID3D11RasterizerState ，状态描述中FillMode设为D3D11_FILL_WIREFRAME即可

 //设置为线框绘制模式

     D3D11_RASTERIZER_DESC rsDesc;

     ZeroMemory(&rsDesc, sizeof(rsDesc));

     rsDesc.CullMode = D3D11_CULL_BACK;

     rsDesc.DepthClipEnable = true;

     //D3D11_FILL_WIREFRAME以线框模式绘制，D3D11_FILL_SOLID是以实体模式绘制

     rsDesc.FillMode = D3D11_FILL_WIREFRAME;

     rsDesc.FrontCounterClockwise = false;

     ID3D11RasterizerState *rsState(nullptr);

     m_pd3dDevice->CreateRasterizerState(&rsDesc, &rsState);

     m_pImmediateContext->RSSetState(rsState);

　　源码下载：http://files.cnblogs.com/files/zhangbaochong/GeoDrawDemo.zip

Directx11学习笔记【十五】基本几何体的绘制的更多相关文章

python3.4学习笔记(十五) 字符串操作（string替换、删除、截取、复制、连接、比较、查找、包含、大小写转换、分割等）
python3.4学习笔记(十五) 字符串操作(string替换.删除.截取.复制.连接.比较.查找.包含.大小写转换.分割等) python print 不换行(在后面加上,end=''),prin ...
(转载)西门子PLC学习笔记十五-（数据块及数据访问方式）
一.数据块数据块是在S7 CPU的存储器中定义的,用户可以定义多了数据块,但是CPU对数据块数量及数据总量是有限制的. 数据块与临时数据不同,当逻辑块执行结束或数据块关闭,数据块中的数据是会保留住的 ...
(C/C++学习笔记) 十五. 构造数据类型
十五. 构造数据类型 ● 构造数据类型概念 Structured data types 构造数据类型结构体(structure), 联合体/共用体 (union), 枚举类型(enumeration ...
MySQL学习笔记十五：优化(2)
一.数据库性能评测关键指标 1.IOPS:每秒处理的IO请求次数,这跟磁盘硬件相关,DBA不能左右,但推荐使用SSD. 2.QPS:每秒查询次数,可以使用show status或mysqladmin ...
Java基础学习笔记十五集合、迭代器、泛型
Collection 集合,集合是java中提供的一种容器,可以用来存储多个数据. 在前面的学习中,我们知道数据多了,可以使用数组存放或者使用ArrayList集合进行存放数据.那么,集合和数组既然都 ...
angular学习笔记(十五)-module里的'服务'
本篇介绍angular中的模块:module 在笔记(二)http://www.cnblogs.com/liulangmao/p/3711047.html里已经讲到过模块,这篇主要讲模块的 '服务' ...
Java学习笔记十五:Java中的成员变量和局部变量
Java中的成员变量和局部变量一:成员变量: 成员变量在类中定义,用来描述对象将要有什么成员变量可以被本类的方法使用,也可以被其他类的方法使用,成员变量的作用域在整个类内部都是可见的二:局部变量 ...
MYSQL进阶学习笔记十五：MySQL 的账号权限赋予！（视频序号：进阶_33，34)
知识点十六:MySQL的账号权限赋予(33) 一.MySQL权限简介关于mysql的权限简单的理解就是mysql允许你做你全力以内的事情,不可以越界.比如只允许你执行select操作,那么你就不能执 ...
数据结构和算法学习笔记十五:多路查找树(B树)
一.概念 1.多路查找树(multi-way search tree):所谓多路,即是指每个节点中存储的数据可以是多个,每个节点的子节点数也可以多于两个.使用多路查找树的意义在于有效降低树的深度,从而 ...
JavaScript权威设计--JavaScript脚本化文档Document与CSS(简要学习笔记十五)
1.Document与Element和TEXT是Node的子类. Document:树形的根部节点 Element:HTML元素的节点 TEXT:文本节点 >>HtmlElement与 ...

随机推荐

plsql导入一个目录下全部excel
import java.io.File; import java.util.ArrayList; import jxl.Sheet; import jxl.Workbook; import com.j ...
oracle 之内存—鞭辟近里（四）
oracle 之内存—鞭辟近里(四) 今天是2013-07-11日,首先我非常感谢我的哥们也是我的网友杨工,非常感谢他能在大数据库内帮我执行一下我所需要的信息.就是他说的网络真是一个互助友爱的平台. ...
GitHub基本操作(转)
一.上传代码到仓库步骤一:创建本地仓库,如下: 创建结果: 步骤二:发布自己创建的仓库,如下: 发布完显示如下: 步骤三:向自己发布仓库上传代码,如下: 首先将代码复制到本地仓库,如下: 复制完,显 ...
UVA 11768 - Lattice Point or Not（数论）
UVA 11768 - Lattice Point or Not option=com_onlinejudge&Itemid=8&page=show_problem&categ ...
我的EJB学习历程
http://blog.csdn.net/sinapaper/archive/2004/06/28/28659.aspx http://blog.csdn.net/sinapaper/archive/ ...
2014鞍山现场赛C题HDU5072（素筛+容斥原理）
Coprime Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others) Total ...
优秀Java程序员必须了解的GC工作原理（转）
一个优秀的Java程序员必须了解GC(Garbage Collection 垃圾收集)的工作原理.如何优化GC的性能.如何与GC进行有限的交互,因为有一些应用程序对性能要求较高,例如嵌入式系统.实时系 ...
Hdu 4539 【状态DP】.cpp
题意: 一个炮兵可以攻打和他之间曼哈顿距离为2的士兵,给出你一块n*m的战场,告诉你哪些地方可以站人哪些地方不可以,问你最多可以安放多少个士兵? n <= 100, m <= 10 思路: ...
[C++/CLI编程宝典][2]什么是C++/CLI语言
对于什么是C++/CLI,我们首先能够简单的将其名字划分为两部分来理解,第一,C++,我们熟悉的眼下被广泛使用的面向对象的ISO国际标准的高级语言,也称为ISOC++,我们这里以后均称其为ISOC++ ...
getline与get函数的区别
get()函数相对getline来说使用方法要灵活的多了. 1. int get()是指从流中抽取单个字符并返回,这个是没有參数的形式.由于c++不像c语言使用getchar() 2.istrea ...

Directx11学习笔记【十五】 基本几何体的绘制

1.基本几何体绘制方法

1.1网格

1.2立方体

1.3圆柱

1.4球

2.场景绘制

2.1最终效果

2.2多个几何体共享顶点索引缓冲区

2.3设为线框模式绘制

Directx11学习笔记【十五】 基本几何体的绘制的更多相关文章

随机推荐

热门专题

Directx11学习笔记【十五】基本几何体的绘制

1.基本几何体绘制方法　

Directx11学习笔记【十五】基本几何体的绘制的更多相关文章