Gcd&Exgcd算法学习小记

Preface

　　对于许多数论问题，都需要涉及到Gcd，求解Gcd，常常使用欧几里得算法，以前也只是背下来，没有真正了解并证明过。

　　对于许多求解问题，可以列出贝祖方程：ax+by=Gcd(a,b)，用Exgcd解之即可到答案，Exgcd即扩展欧几里得算法。他还能求乘法逆元，同余方程通解。没有你想得到的，只有你做不到的。

　　这里是对于两个算法的学习小记

Content

欧几里得算法

算法介绍

　　由百度百科得

　　欧几里德算法又称辗转相除法，用于计算两个正整数a，b的最大公约数。

　　从整数的除法可知:对任给二整数a,b0,必有二整数q及r存在,使得a=qb+r,0≤rb,并且q及r是唯一存在的,这是数论的一条基本定理,整数的一系列重要性质都可以由此得到,如果反复利用这一基本定理,就可以得到因为每进行一次除法,余数就至少减一,而b是有限的正整数,所以最多进行b次,总可以得到一个余数是零的等式,即rn+1=0。

　　当然，百度说的这种话我都是看不懂的。

　　其实辗转相除法就是运用了Gcd(a,b)=Gcd(b,a mod b)，直到a≡0（mod b），b即为所求。

　　这个方法的目的是为了达到可以将求解的两个数不断缩小，使得效率为对数级别。

算法证明

　　那么，我们如何求证这个式子的正确性呢？

　　我们令

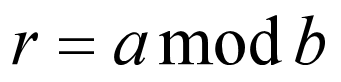
　　根据模运算的定义，可以有

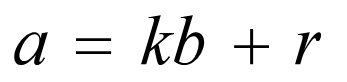
　　移项可得

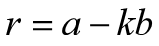
　　令d为a,b公约数，可有

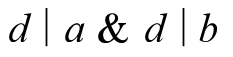
　　根据我的思考，得出拥有公约数的两个数相减，其差必定能整除这个公约数，用乘法分配律易证。由这个东东，我们知道d一定是a,kb的公约数，故可得　

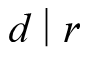
　　综上所瞎BB，因为d|b,d|a mod b，所以b和a mod b有公约数d，又因为d为a,b公约数，所以a,b,a mod b都包含约数d

　　上面的d为任意一个，当d为a,b的最大公约数，根据上面所说，此时b和a mod b一定也包含公约数d

算法实现

　　自此，我们证了欧几里得几千年前就会证的东西。用现代化语言来描述这古老的知识是这样的

扩展欧几里得算法　　

算法简介　　

　　按照惯例，看看大佬们怎么说。由百度百科得

　　扩展欧几里得算法是欧几里得算法（又叫辗转相除法）的扩展。除了计算a、b两个整数的最大公约数，此算法还能找到整数x、y（其中一个很可能是负数）。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。有两个数a,b，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到ax+by=gcd(a,b)的整数解。

　　这篇百度百科用了列式子，作诠释的说明方法，让我明白了许多，表达了作者写时凉凉的心情。

　　自从会证欧几里得算法之后，这一切的一切变得更加明朗蒙蔽

　　说白了，扩展欧几里得就是扩展的，运用某些欧几里得算法的东西来解出关于x,y的方程ax+by=gcd(a,b)的通解。但是一般没有几个身体健康的出题人会让你求这个无聊的东西。所以这个东西一般应用于求方程的某个特殊解亦或者求乘法逆元。

算法核心

　　我们看看它是怎么操作的，显然有

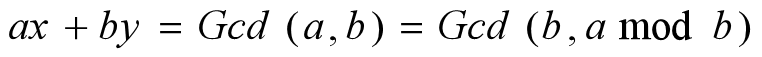
　　我们令，显然等于我头上的这个式子

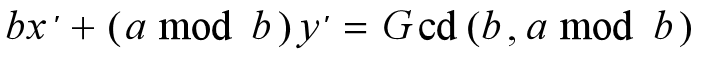
　　我们将上面左式根据模定义升级得到

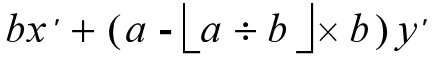
　　我们将y′代进括号里，再提取b，得

　　我们再看看上面的连等式ax+by，他们是等价的，根据恒等定理有

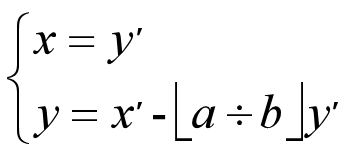
　　但是我们知道这个有什么用呢？我们又不知道他们其中任何一个值，根本求不出x和y。

　　我们需要冷静一下，x,y是在ax+by=Gcd(a,b)时的解。x′,y′是在gcd(b,a mod b)=bx′+(a mod b)y′时的解，那么

　　这既然是扩展的，必定与欧几里得有不可告人的关系。gcd在最后是当gcd(a,0)=a时，求出最大公约数。那么当b=0时，我们带进去ax+by=Gcd(a,b)里面算，其实就是ax=a，那么x必定为1.b不可知，我们可以将b视为0，那么此时x,y的一个解就是

　　我们既然知道了这个，我们根据上面x,y与x′,y′的关系式，推算出x,y的值，不断递归回去，继而得出满足贝祖方程的一个解。因为这个方程必定有规律可循，所以我们对这个解进行某些变换，即可得出这个方程的通解，这是显然又必然的。

算法实现

　　实现起来和欧几里得算法有异曲同工之妙，可以说我们比欧几里得厉害，因为他不会编程；

算法扩展

扩展一：乘法逆元

　　对于形如这个样的式子，我们称x是a关于b的乘法逆元

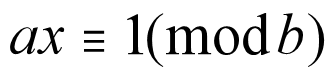
　　这个式子的本质就是

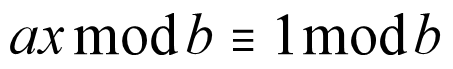　　脑补得到

　　如果这个式子有关于x,y的整数解，那么a,b 必定互质。为什么？

　　如果a,b不互质，那么他们必定有公约数。那么根据上面所说，拥有公约数的两个数相减，其差必定能整除这个公约数，然而1并不是一个大于1的公约数，所以得证。

　　因为y是未知的，我们可以将y视为相反数，那么符号可以变为正，而扩展gcd又可以解负数，其颜值越来越像贝祖公式了。又因为gcd(a,b)=1，所以得到

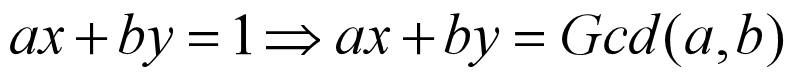
　　一不小心又可以用扩展欧几里得来解了。显然可以求出x的值，x的值即为乘法逆元。对于这种a,b互质的同余方程，一般只有唯一解。当然，会有无解的情况。根据一个定理来判断：ax+by=c，那么gcd(a,b)丨c，不然的话无解。

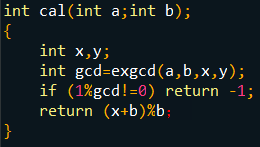
扩展二：求解方程ax+by=c

　　这个与上面类似。因为gcd(a,b)丨c，所以我们可以用扩展欧几里得先求出ax+by=gcd(a,b)

　　如何求目前这个方程的通解？假设我们求出了对于关于x,y的方程ax+by=gcd(a,b)的一组解为x0，y0，我们带入可以得到

　　ax0+by0=gcd(a,b)，继而还有a(x0+b)+b（y0-a)，a(x0+2*b)+b（y0-2*a)，因为这样乘出来还是ax0+by0，所以可行

　　所以通解为x=x0+k*b;y=y0-k*a;

　　我们再看回原来的方程ax+by=c，发现其实类似，可以自己思考。

经典例题

　　[ZJOI2002] 青蛙的约会 →题解
　　[Vijos1009] 清帝之惑之康熙 →题解
　　[NOIP2012] 同余方程 →题解
　　[poj2115] C Looooops →题解
　　[poj2891] Strange Way to Express Integers →题解
　　[hdu1573] X问题 →题解
　　[hdu3579] Hello Kiki →题解
　　[poj2142] 天平 The Balance →题解 
　　[poj1091] 跳蚤 →题解

　　[bzoj2242][SDOI2011]计算器