HDU 2174 Bridged Marble Rings

题目：Bridged Marble Rings

链接：http://acm.hdu.edu.cn/showproblem.php?pid=2174

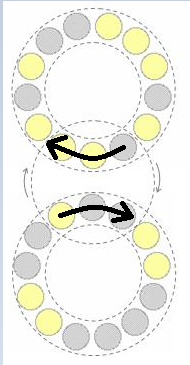
题意：如图，要把所有灰色球移动到上圈，每次操作可以转图中虚线圈起的三个圆，求中间圆的最少转数。题目给出的是字符串，g代表灰色球，y代表黄色球，起始位置看标记。

思路：

　　BFS打表+最小表示法

　　令g=1，y=0，用int 表示当前状态。

　　最开始直接用BFS打表，超时超内存，按我最初的算法，所有状态总数为C（26，13）约等于1000多万种。但实际上，因为转动上下两个圈是不增加转数的，所以很多情况是等价的，可以压缩状态数，对于一个状态S，可以转动上圈，下圈使其得到最小表示的状态T。接着存T就可以了。每次，注意，map会超时，后面我改成哈希就过了。。。

　　具体：每次出队一个状态，将该状态对应的13*13个下一步状态（筛选一下）入队。

AC代码：

 #include<stdio.h>
 #include<map>
 #include<queue>
 #include<algorithm>
 using namespace std;

 #define Mod 1000007     //取模的大小，哈希表的大小...
 #define Max 100007         //存放的总数
 typedef long long LL;
 class Hash             //手写哈希
 {
   public:
     int hs[Mod];       //哈希值  设定的哈希函数为 原值 % Mod ，所以哈希值有可能是 0 ~ Mod-1
     int next[Max];     //链表    存放哈希值相等的一条链，他的大小取决于所有原值的数量
     LL S[Max];         //存放原值
     int H[Max];        //存放所有哈希值
     int sn;            //不同原值的数量
     int hn;            //不同哈希值的数量
     Hash()             //构造函数: 定义Hash类变量时初始化
     {
       sn=;
       hn=;
       for(int i=;i<Mod;i++)
         hs[i]=;
     }
     void clear()       //清空函数
     {
       sn=;
       for(int i=;i<hn;i++)
         hs[H[i]]=;
       hn=;
     }
     void add(LL s)           //加入
     {
       int ha=abs(s)%Mod;     //计算哈希值
       if(hs[ha]==)          //如果该哈希值还未出现过
       {
         H[hn++]=ha;          //将该哈希值记录起来，同时哈希值数量加 1
       }
       sn++;                  //0 表示结尾，所以从1 开始存，原值数量加 1，特别针对 hs数组
       S[sn]=s;               //将原值记录起来
       next[sn]=hs[ha];       //原本原值记录位置
       hs[ha]=sn;             //最新原值记录位置，如果从0 开始存，就无法判断此时是空还是1个值
       //比如：5 和 10 有一样的哈希值 ，并且 5 和 10 先后加入 那么有：
       //5 加入: next[1] = 0; hs[5] = 1; hs[5] 是哈希值为5 的头，表示第一个原值在1的位置
       //10加入: next[2] = 1; hs[5] = 2; 表示第一个哈希值为5的在2，第二个在1，第三个不存在
     }
     int find(LL s)           //查找
     {
       int ha=abs(s)%Mod;     //计算哈希值
       int k=hs[ha];          //头
       while(k!=)
       {
         if(S[k]==s) return k;//找到
         k=next[k];           //下一个节点
       }
       return ;              //表示没找到
     }
 };

 int move(int s, int i){
   int gao = (s>>)&0x1FFF;
   int di = s&0x1FFF;
   if(i==){
     int tmp = di&;
     di = di >> ;
     di = di | (tmp << );
   }
   else if(i==){
     int tmp = gao&;
     gao = gao >> ;
     gao = gao | (tmp << );
   }
   else{
     int a = (gao & 0x1C00)>>;
     int b = (di & 0x1C00)>>;
     gao = gao & 0x3FF;
     di = di & 0x3FF;
     gao = (b<<)| gao;
     di = (a<<) | di;
   }
   return (gao<<)|di;
 }

 map<int, int> mp;
 int c[<<];

 int min_code(int s){
   int gao = (s>>)&0x1FFF;
   int di = s&0x1FFF;
   gao = c[gao];
   di = c[di];
   return (gao<<)|di;
 }
 int min_code_1(int s){
   int ms=s;
   for(int i=; i<; i++){
     int tmp = s&;
     s >>= ;
     s = s | (tmp << );
     if(ms>s) ms=s;
   }
   return ms;
 }

 Hash hs;
 queue<int> q;

 void mov(int ms){
   int a=ms;
   for(int i=; i<; i++){
     a=move(a, );
     int b=a;
     for(int j=; j<; j++){
       b=move(b, );
       int c=move(b, );
       int mc=min_code(c);
       int cx=hs.find(mc);
       if(cx==){
         hs.add(mc);
         mp[mc]=mp[ms]+;
         q.push(mc);
       }
     }
   }
 }

 void bfs(int s){
   s=min_code(s);
   mp[s]=;
   q.push(s);
   while(q.size()){
     int a=q.front();
     q.pop();
     mov(a);
   }
 }

 int main(){
   for(int i=; i<(<<); i++){
     c[i]=min_code_1(i);
   }
   int t=0x3FFE000;
   bfs(t);
   char tmp[];
   while(~scanf("%s", tmp)){
     int s=;
     for(int i=; tmp[i]; i++){
       if(tmp[i]=='g') s=s*+;
       else s=s*;
     }

     if(s==t) printf("0\n");
     else printf("%d\n", mp[min_code(s)]-);
   }
   return ;
 }