POJ-3169 Layout---差分约束系统+Bellman

题目链接：

https://vjudge.net/problem/POJ-3169

题目大意：

一些母牛按序号排成一条直线。有两种要求，A和B距离不得超过X，还有一种是C和D距离不得少于Y，问可能的最大距离。如果没有输出-1，如果可以随便排输出-2，否则输出最大的距离。

Sample Input

4 2 1
1 3 10
2 4 20
2 3 3

Sample Output

27

思路：

设xi为第i头牛的x坐标

对于第一种要求，A和B之间距离不超过X（题目中A<B）

那就有:xB - xA <= X

对于第二种要求，A和B之间距离少于X（题目中A<B）

那就有:xB - xA >= X

对于上述两种不等式，可知这道题就是一堆不等式组，可以用差分约束系统来做。

u是起点，v是终点

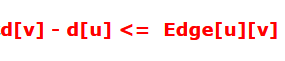
对于第一种不等式，转化成A->B的边，权值为X

对于第二种不等式，先转化成上述形式，xA - xB <= -X，转化成B->A的边，权值是-X

在题目中隐含了一组不等式xi-1<=xi，转化成上述形式就是xi-1 - xi <= 0，边为i -> i-1权值是0

然后要看题目中求的是什么：

求的是从1到n的最大距离

就等价于xn-x1最大

等价于xn-x1 <= M需要求M的最小值（因为M没有最大值，最大值是正无穷）

这个不等式就是1到n的边，权值为M，说明题目求的是1到n的最短路，如果存在负环，输出-1，如果是INF输出-2，否则输出最短路长度。分析到这里就可以套模板啦

 #include<iostream>
 #include<vector>
 #include<queue>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 using namespace std;
 typedef pair<int, int> Pair;
 const int maxn =  + ;
 const int INF = 0x3f3f3f3f;
 int T, n, m, m1, m2;
 struct edge
 {
     int u, v, w;
     edge(int u, int v, int w):u(u), v(v), w(w){}
     edge(){}
 };
 edge e[maxn];
 int d[], tot;
 void addedge(int u, int v, int w)
 {
     e[tot++] = edge(u, v, w);
 }
 bool Bellman()
 {
     int u, v, w;
     memset(d, INF, sizeof(d));
     d[] = ;
     for(int j = ; j < n; j++)
     {
         for(int i = ; i < tot; i++)
         {
             u = e[i].u, v = e[i].v,  w = e[i].w;
             if(d[u] < INF && d[v] > d[u] + w)
             {
                 d[v] = d[u] + w;
                 if(j == n - )return true;//存在负环,方程组无解
             }
         }
     }
     return false;
 }
 int main()
 {
     cin >> n >> m1 >> m2;
     int u, v, w;
     for(int i = ; i < m1; i++)//第一组边，u->v 权值w
     {
         scanf("%d%d%d", &u, &v, &w);
         addedge(u, v, w);
     }
     for(int i = ; i < m2; i++)//第二组边 v->u 权值-w
     {
         scanf("%d%d%d", &u, &v, &w);
         addedge(v, u, -w);
     }
     for(int i = ; i < n; i++)//第三组边 i+1->i 权值0
         addedge(i + , i, );
     if(Bellman())
     {
         cout<<"-1"<<endl;
     }
     else
     {
         if(d[n] == INF)cout<<"-2"<<endl;
         else cout<<d[n]<<endl;
     }
     /*for(int i = 1; i <= n; i++)
     {
         cout<<i<<":::";
         for(int j = 0; j < G[i].size(); j++)cout<<G[i][j].v<<"-"<<G[i][j].w<<"   ";
         cout<<endl;
     }*/
 }