洛谷P2480 [SDOI2010]古代猪文

要求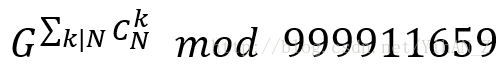（图是盗来的QAQ）

首先用欧拉定理把幂模一下，直接就是MOD-1了

然后发现MOD-1可以分解为2,3,4679,35617，都是质数，可以直接用Lucas定理

然后用中国剩余定理合并一下即可

千万不可把MOD和MOD-1搞混了，否则调试好麻烦的

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 #include<cmath>
 #define MAXN 35617+10
 #define ll long long
 #define pb push_back
 #define ft first
 #define sc second
 #define mp make_pair
 using namespace std;
 ll c[],m[]={,,,,};
 ll MOD=;
 ll N,G;
 ll inv[MAXN],finv[MAXN],fac[MAXN];
 ll Pow(ll a,ll b,ll p){
     ll ret=1LL;
     while(b){
         if(b&){
             (ret*=a)%=p;
         }
         (a*=a)%=p;
         b>>=;
     }
     return ret;
 }
 ll Inv(ll x,ll p){
     return Pow(x,p-,p);
 }
 ll C(ll n,ll m,ll p){
     if(n<m)return 0LL;
     return fac[n]*finv[m]*finv[n-m]%p;
 }
 ll Lucas(ll n,ll m,ll p){
     if(!m)return 1LL;
     if(n>=p||m>=p){
         ll nn=n%p,mm=m%p;
         if(nn<mm)return 0LL;
         return Lucas(n/p,m/p,p)*C(nn,mm,p)%p;
     }
     else{
         return C(n,m,p);
     }
 }
 ll solve(ll p){
     fac[]=fac[]=;
     finv[]=finv[]=;
     inv[]=;
     for(int i=;i<p;i++){
         fac[i]=fac[i-]*i%p;
         inv[i]=p-(inv[p%i]*(p/i)%p);
         finv[i]=finv[i-]*inv[i]%p;
     }
     ll t=sqrt(1.0*N);
     ll ret=0LL;
     for(ll i=;i<=t;i++){
         if(N%i==){
             ret+=Lucas(N,i,p);
             if(N/i!=i){
                 ret+=Lucas(N,N/i,p);
             }
         }
     }
     return ret;
 }
 ll CRT(){
     ll M=MOD-;
     ll ret=0LL;
     for(int i=;i<=;i++){
         ll t=Inv(M/m[i],m[i])%M*(M/m[i])%M;
         ret+=t*c[i]%M;
         ret%=M;
     }
     return ret;
 }
 int main()
 {
     scanf("%lld%lld",&N,&G);
     if(G%MOD==){
         printf("0\n");
         return ;
     }
     for(int i=;i<=;i++) c[i]=solve(m[i]);
     ll x=CRT();
     ll ans=Pow(G,x,MOD);
     printf("%lld\n",ans);
 }