R--线性回归诊断（一）

线性回归诊断--R

【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

Ljt   勿忘初心  无畏未来

作为一个初学者，水平有限，欢迎交流指正。

---

在R中线性回归，一般使用lm函数就可以得到线性回归模型，但是得到的模型到底合不合适？在我们使用所得到的线性模型之前就需要进行回归诊断。

线性回归的诊断，主要是检验线性回归模型的假设是否成立。

线性回归模型    y=Θ₀+Θ₁x₁+Θ₂x₂+.......+Θ_mx_m+ε    （自变量与因变量之间是线性关系）

基本假设：

（1）随机干扰项 ε 服从零均值，同方差，零协方差（相互独立）的正态分布

E(ε_i)=0  ;   var(ε_i)=σ²   ;   cov(ε_i , εj)=0     ;

ε_i~N(0,σ²)

（2）随机干扰项 ε 与解释变量间不相关

cov(X_i , ε_i) =0

---

（一）显著性检验

（1）回归方程显著性 F 检验 ： 看自变量 X₁ , X₂ .....X_m  从整体上对随机变量Y是否有明显的影响 。

原假设 H₀：Θ₁ =Θ₂=.....=Θ_m=0        （H₀ 若被接受则表明随机变量Y与X₁ , X₂ .....X_m 之间的关系由线性回归模型表示不合适）

P值<α  :  拒绝原假设 。即在显著性水平 α 下，Y 与 X₁ , X₂ .....X_m 有显著的线性关系，回归方程是显著的。（自变量全体对因变量产生线性影响）

（2）回归系数显著性 t 检验：看单个的自变量 X_i 对Y是否有明显影响。

原假设   H_0i ：Θ_i =0            （H_0i 若被接受则表明自变量X_i 对因变量Y的线性效果不显著）

P值<α  :   拒绝原假设 。即在显著性水平 α 下，Y 与 X_i 有显著的线性关系。

对于一元线性回归这两种检验是等价的；

对于多元线性回归，这两种检验是不等价的:

F检验显著，说明Y对自变量X₁ , X₂ .....X_m 整体的线性回归效果是显著的，但不等于Y对每个自变量X_i 的效果都显著;反之，某个或某几个X_i 的系数不显著，回归方程显著性的F检验仍然有可能是显著的。由于某些自变量不显著，因而在多元回归中并不是包含在回归方程中的自变量越多越好，需要剔除对Y无显著影响的自变量。

（二）拟合优度

拟合优度用于检验回归方程对样本观测值的拟合程度。

样本决定系数 R² = SSR/SST = 1 - SSE/SST      （R²属于[0,1] ）

R² 越接近 1 ，表明回归拟合的效果越好；

R² 越接近 0 ，表明回归拟合的效果越差。

与F检验相比，R² 可以更清楚直观地反映回归拟合的效果，但是并不能作为严格的显著性检验。需要指出的是，拟合优度并不是检验模型优劣的唯一标准，有时为了使模型从结构上有较合理的经济解释，在样本量n 较大时，R² 等于0.7左右我们也给回归模型以肯定态度。需要注意的是 R²与回归方程汇中自变量的数目以及样本量n有关，当样本量n与自变量的个数接近时，R²易接近于1，其中隐含着一些虚假的成分。

---

下面结合实例对R语言中线性拟合函数lm的结果进行分析

>
>
> head(bank)
       y     x1     x2    x3     x4
1 1018.4  96259 2239.1 50760 1132.3
2 1258.9  97542 2619.4 39370 1146.4
3 1359.4  98705 2976.1 44530 1159.9
4 1545.6 100072 3309.1 39790 1175.8
5 1761.6 101654 3637.9 33130 1212.3
6 1960.8 103008 4020.5 34710 1367.0
>
> fline<-lm(y~x1+x2+x3+x4,data=bank)
> summary(fline)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = bank)

Residuals:
    Min      1Q  Median      3Q     Max
-487.35  -78.89   -2.65  137.02  403.78 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.168e+03  1.193e+03  -3.495 0.002998 **
x1           5.842e-02  1.216e-02   4.805 0.000194 ***
x2           4.142e-01  3.218e-02  12.871 7.41e-10 ***
x3          -1.384e-02  8.520e-03  -1.624 0.123826
x4          -7.062e-01  1.750e-01  -4.035 0.000959 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 217.7 on 16 degrees of freedom
Multiple R-squared:  0.9982,	Adjusted R-squared:  0.9978
F-statistic:  2222 on 4 and 16 DF,  p-value: < 2.2e-16

>
>

　　

回归结果的诊断：

（1）F-statistic

回归方程显著性 F 检验中的F统计量，其P值<2.2e-16<0.05 ，表明Y 与 X₁ , X₂ ,X₃,X₄有显著的线性关系，回归方程整体是显著的。

（2）Coefficients

Estimate 即回归系数的估计值，其对应的 P(>|t|)为各回归系数t检验的P值。

从回归结果看，X3的P值为0.123826>0.05,表明X3对Y没有显著影响，应考虑删除变量X3；其他三个变量的P值都<0.05,对Y 都有显著的影响。

---------以上两个回归检验的结果也表明，自变量整体对于因变量有显著影响，并不表明每个自变量对因变量都有显著影响。

（3）Multiple R-squared  ;   Adjusted R-squared

分别表示 ‘拟合优度’  ，‘修正的拟合优度’

拟合优度值为 0.9982  很接近于 1 ，表明回归方程对样本观测值的拟合程度较高。

---

相关图形诊断：

（1）残差图

残差图分析法是一种直观、方便的分析方法。它以残差e_i 为纵坐标，以其他适宜的变量（如样本拟合值）为横坐标画散点图,主要用来检验是否存在异方差。

一般情况下，当回归模型满足所有假定时，残差图上的n个点的散布应该是随机的，无任何规律。如果残差图上的点的散布呈现出一定趋势（随横坐标的增大而增大或减小），则可以判断回归模型存在异方差。

异方差：某一因素或某些因素随着解释变量观测值的变化而对被解释变量产生不同的影响，导致随机误差产生不同方差。

当存在异方差时，普通最小二乘估计存在以下问题：

（i）  参数估计值虽然是无偏的，但不是最小方差线性无偏估计；

（ii） 参数的显著性检验失效；

（iii） 回归方程的应用效果极不理想。

（2）Q-Q图

Q-Q图主要用来检验样本是否近似服从正态分布。

对于标准状态分布而言，Q-Q图上的点近似在Y=X直线附近。

（3）标准化残差方根散点图

此图类似于残差图，只是其纵坐标变为了标准化残差的绝对值开方。

（4）Cook距离图

库克距离用来判断强影响点是否为Y的异常值点。

一般认为  当D<0.5时认为不是异常值点；当D>0.5时认为是异常值点。

>
> par(mfrow=c(2,2))
> plot(fline,which=c(1:4))
>

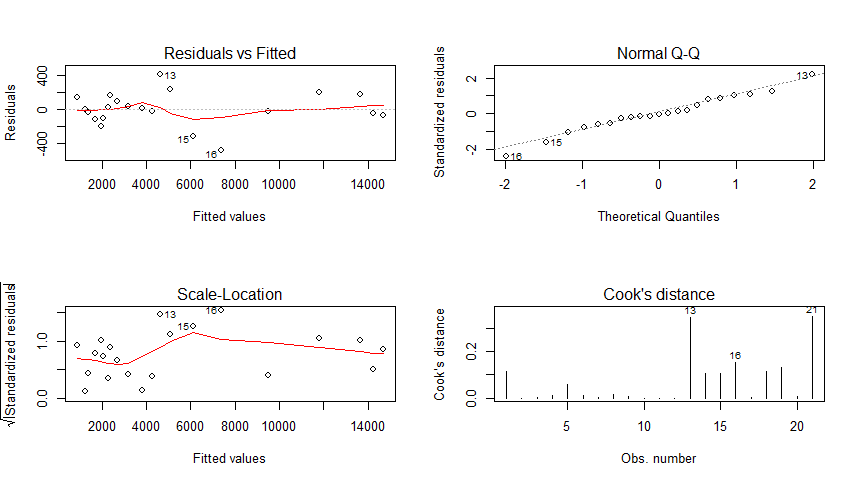
从回归的四个图形结果来看：

残差图   Residuals vs Fitted  :  图上的点基本服从随机分布，可以认为不存在异方差的情况；

标准Q-Q图  Normal Q-Q       :  图上的点基本都在y=x直线附件，可认为样本近似服从正态分布；

标准化残差方根散点图 Scale-Location：类似与残差图，点的分布基本是随机的。

库克距离图 Cook‘s distance   :  最大的库克距离为0.3左右，可以认为没有异常值点。

---