Boosting 和梯度Boosting

Boosting方法：

Boosting这其实思想相当的简单，大概是，对一份数据，建立M个模型（比如分类），一般这种模型比较简单，称为弱分类器(weak learner)每次分类都将上一次分错的数据权重提高一点再进行分类，这样最终得到的分类器在测试数据与训练数据上都可以得到比较好的成绩。

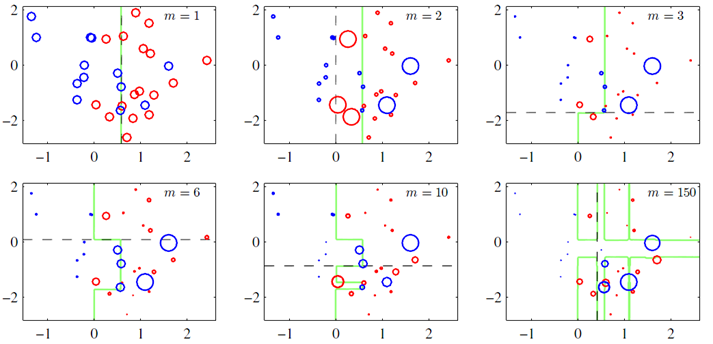
上图（图片来自prml p660）就是一个Boosting的过程，绿色的线表示目前取得的模型（模型是由前m次得到的模型合并得到的），虚线表示当前这次模型。每次分类的时候，会更关注分错的数据，上图中，红色和蓝色的点就是数据，点越大表示权重越高，看看右下角的图片，当m=150的时候，获取的模型已经几乎能够将红色和蓝色的点区分开了。

Boosting可以用下面的公式来表示：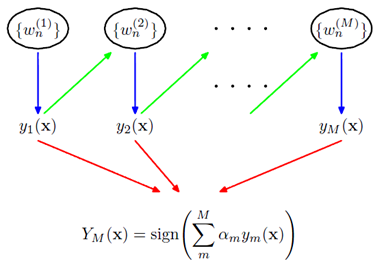

训练集中一共有n个点，我们可以为里面的每一个点赋上一个权重Wi(0 <= i < n)，表示这个点的重要程度，通过依次训练模型的过程，我们对点的权重进行修正，如果分类正确了，权重降低，如果分类错了，则权重提高，初始的时候，权重都是一样的。上图中绿色的线就是表示依次训练模型，可以想象得到，程序越往后执行，训练出的模型就越会在意那些容易分错（权重高）的点。当全部的程序执行完后，会得到M个模型，分别对应上图的y1(x)…yM(x)，通过加权的方式组合成一个最终的模型YM(x)。

我觉得Boosting更像是一个人学习的过程，开始学一样东西的时候，会去做一些习题，但是常常连一些简单的题目都会弄错，但是越到后面，简单的题目已经难不倒他了，就会去做更复杂的题目，等到他做了很多的题目后，不管是难题还是简单的题都可以解决掉了。

Gradient Boosting方法：

其实Boosting更像是一种思想，Gradient Boosting是一种Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型损失函数的梯度下降方向。这句话有一点拗口，损失函数(loss function)描述的是模型的不靠谱程度，损失函数越大，则说明模型越容易出错（其实这里有一个方差、偏差均衡的问题，但是这里就假设损失函数越大，模型越容易出错）。如果我们的模型能够让损失函数持续的下降，则说明我们的模型在不停的改进，而最好的方式就是让损失函数在其梯度（Gradient)的方向上下降。

下面的内容就是用数学的方式来描述Gradient Boosting，数学上不算太复杂，只要潜下心来看就能看懂：）

    可加的参数的梯度表示：

假设我们的模型能够用下面的函数来表示，P表示参数，可能有多个参数组成，P = {p0,p1,p2….}，F(x;P)表示以P为参数的x的函数，也就是我们的预测函数。我们的模型是由多个模型加起来的，β表示每个模型的权重，α表示模型里面的参数。为了优化F，我们就可以优化{β,α}也就是P。

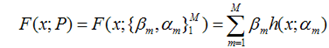
我们还是用P来表示模型的参数，可以得到，Φ(P)表示P的likelihood函数，也就是模型F(x;P)的loss函数，Φ(P)=…后面的一块看起来很复杂，只要理解成是一个损失函数就行了，不要被吓跑了。

  
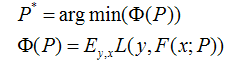
既然模型(F(x;P))是可加的，对于参数P，我们也可以得到下面的式子：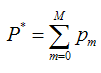  
这样优化P的过程，就可以是一个梯度下降的过程了，假设当前已经得到了m-1个模型，想要得到第m个模型的时候，我们首先对前m-1个模型求梯度。得到最快下降的方向，gm就是最快下降的方向。

   
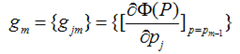
这里有一个很重要的假设，对于求出的前m-1个模型，我们认为是已知的了，不要去改变它，而我们的目标是放在之后的模型建立上。就像做事情的时候，之前做错的事就没有后悔药吃了，只有努力在之后的事情上别犯错：

   
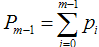
我们得到的新的模型就是，它就在P似然函数的梯度方向。ρ是在梯度方向上下降的距离。

   
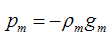
我们最终可以通过优化下面的式子来得到最优的ρ：

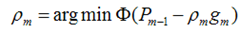
    可加的函数的梯度表示：

上面通过参数P的可加性，得到了参数P的似然函数的梯度下降的方法。我们可以将参数P的可加性推广到函数空间，我们可以得到下面的函数，此处的fi(x)类似于上面的h(x;α)，因为作者的文献中这样使用，我这里就用作者的表达方法：

   
同样，我们可以得到函数F(x)的梯度下降方向g(x)

   
最终可以得到第m个模型fm(x)的表达式:

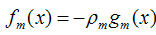
    通用的Gradient Descent Boosting的框架：

下面我将推导一下Gradient Descent方法的通用形式，之前讨论过的：

   
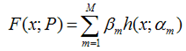
对于模型的参数{β,α}，我们可以用下面的式子来进行表示，这个式子的意思是，对于N个样本点(xi,yi)计算其在模型F(x;α,β)下的损失函数，最优的{α,β}就是能够使得这个损失函数最小的{α,β}。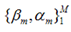
表示两个m维的参数：

   
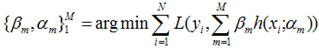
写成梯度下降的方式就是下面的形式，也就是我们将要得到的模型fm(x)的参数{αm,βm}能够使得fm的方向是之前得到的模型Fm-1(x)的损失函数下降最快的方向：

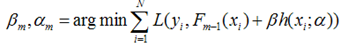
对于每一个数据点xi都可以得到一个gm(xi)，最终我们可以得到一个完整梯度下降方向

   
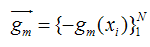
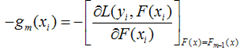
为了使得fm(x)能够在gm(x)的方向上，我们可以优化下面的式子得到，可以使用最小二乘法：

   
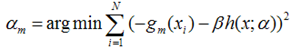
得到了α的基础上，然后可以得到βm。 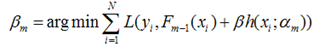      最终合并到模型中：

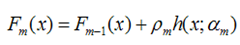
算法的流程图如下

    
之后，作者还说了这个算法在其他的地方的推广，其中，Multi-class logistic regression and classification就是GBDT的一种实现，可以看看，流程图跟上面的算法类似的。这里不打算继续写下去，再写下去就成论文翻译了，请参考文章：Greedy function Approximation – A Gradient Boosting Machine，作者Freidman。