PBR Step by Step（ 五）Phong反射模型

Lamertian模型描述了当光源直接照射到粗糙物体表面时，反射光线的分布情况。在现实中，除了直接光照，还有来自周围环境的间接光照。

直接照射到物体表面的光照，又称为局部光照；

间接照射到物体表面的光照，又称为全局光照。

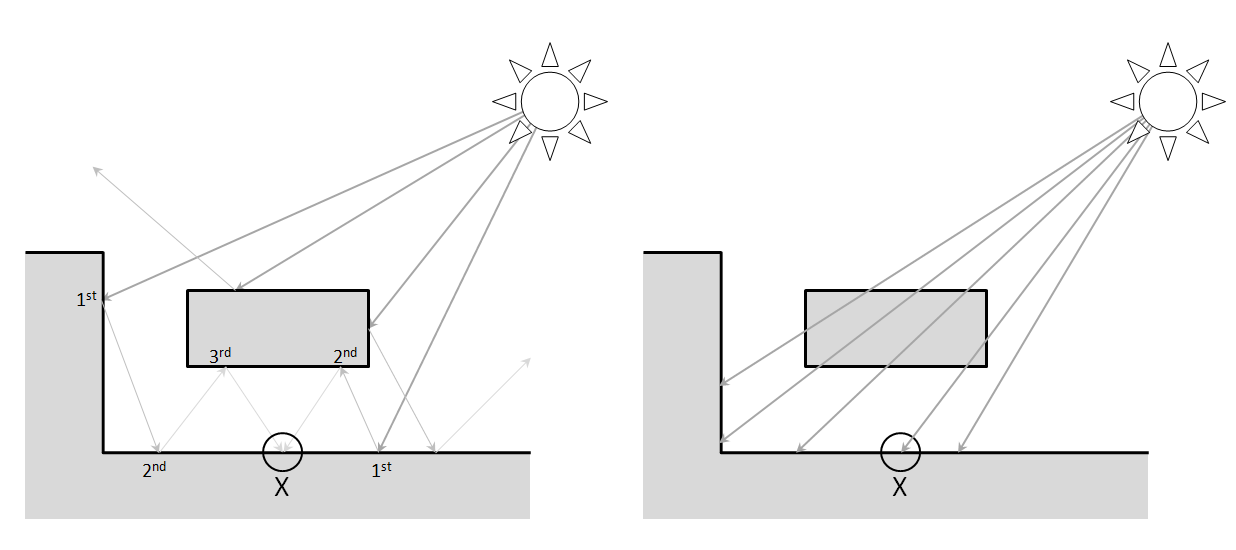
左图中点x接收到周围环境的光线照射，来自周围表面的反射光照称为全局光照；右图中点x接收来自太阳光的直接照射，来自太阳发射的直接光照称为局部光照。

在现实环境中，全局光照的情况更为复杂，例如：

• 半透明表面（Semi-transparent surfaces）：光线可以穿过表面进行复杂的交互，如玻璃棱镜，可以改变光的波长；
• 次表面散射（Sub-Surface Scattering）：光线可以穿过子表面，在同一表面的不同方向反射，如皮肤；
• 表面渗色（Surface bleeding）：光线穿过表面，在介质中改变颜色到目标表面。

其他例子还有很多，全局光照会比局部光照效果更佳柔和自然。我们在前篇中所研究的Lambertain BRDF光照模型为局部光照模型，还欠缺了全局光照因素。

环境光照Ambient

在实时渲染中模拟全局环境光照还是有一定难度的，通常为了不使场景中在没有全局光照射的情况下呈现黑暗，可理想的认为环境光均匀分布在所有物体表面。

即环境光与位置\({p}\)和方向\({\omega_i}\)无关，在所有表面都呈现同一颜色，表示为：

\({L_i} = {l_sc_l}\)

其中，\({l_s}\)表示光照强度系数，\({c_l}\)表示光照颜色。

（未完待续，此处需补充双半球反射率\({\rho_{hh}}\)）

Phong反射模型

Lamertian模型是粗糙表面的理想反射模型，当光线照射到光滑表面会产生高光，Phong反射模型（Phong reflection model，1973）是其中一类的有向光照的镜面反射模型。

根据光的反射定律：入射光线与反射光线成相同角度。

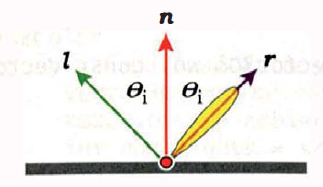
用\({l}\)表示入射光线，\({r}\)表示出射光线，\({n}\)表示物体表面法线，那么存在如下方程关系：

式①：\({r} = {al} + {bn}\)

上式中，\({a}\)和\({b}\)为常数项。对上式左右两边同乘\({n}\)：

\({r \cdot n} = {al \cdot n} + {bn \cdot n}\)

得到式②：\({(1 - a)l \cdot n} = {b}\)

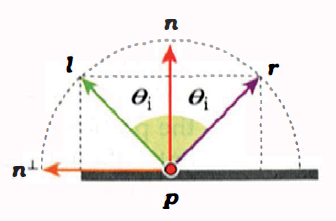
如果用\({n}^{\perp}\)表示与表面法线\({n}\)垂直的向量，那么\({l}\)与\({r}\)在\({n}^{\perp}\)上的投影应为相反的向量，\({r} = -{l}\)：

\({r \cdot n^{\perp}} = {al \cdot n^{\perp}} + {bn \cdot n^{\perp}}\)

\({-l \cdot n^{\perp}} = {al \cdot n^{\perp}}\)

得：\({a} = -1\)

代入式①和式②中，可得\({r}\)的表达式：

\({r} = -{l} + {2(n \cdot l)n}\)

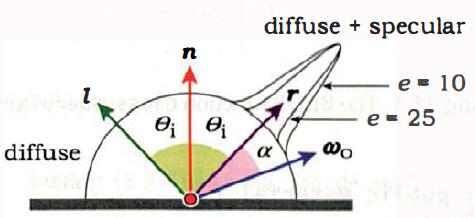
围绕在反射光线\({r}\)附近的反射辐射度应随\({\omega_o}\)与\({r}\)之间的夹角\({\alpha}\)的增加而减少。

Phong模型的镜面反射部分表示为\({\cos \alpha}^{e} = {r \cdot \omega_o}^{e}\)，\(\alpha \in {[0, \frac{\pi}{2}]}\)，\({\cos \alpha} \in {[0, 1]}\)，\({e}\)与\(\alpha\)存在如下函数分布关系：

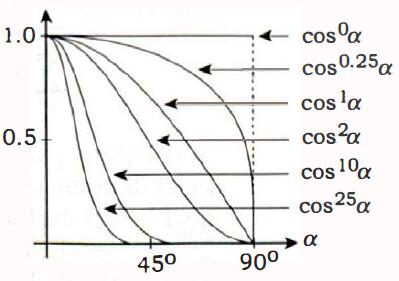
分布图中y轴代表\({e}\)，x轴代表\(\alpha\)，当\({e}\)增大时，随\(\alpha\)的增加而快速收敛。

至此可知Phong的BRDF高光项为：\({f_{r, s}(l, \omega_o)} = {k_s(r \cdot \omega_o)^{e}}\)

其中，\({k_s} \in [0, 1]\)表示为高光系数。

（未完待续）