2019中山大学程序设计竞赛（重现赛） Clumsy Keke

Problem Description

Keke is currently studying engineering drawing courses, and the teacher has taught her how to find its volume through the three views of the part. But her brain doesn't work well that she can't find the volume of complex parts. So she needs your help.

To simplify the problem, the part is made up of cubes with side length 1, and the vertices of these cubes are all on the grid. Give you three 0/1 matrices, each representing each of the three views. 0 means that there is no projection of cubes at this position of the view; 1 means that there is a projection of cubes at this position of the view.

Now Keke wants you to help her find the volume of the part determined by the three views.

Input

There are mutiple test cases, the number of which is no more than 10. For each test case:

The first line of input contains three integers mx,my,mz(1≤mx,my,mz≤99)

, which represent the coordinate range of all possible cubes (i.e. all possible cubes are in the cuboid area whose body diagonal is from (1,1,1)

to (mx,my,mz)

).

Following input a 0/1 matrix with mx

lines and my

columns representing the front view, and the y

-th column of the x

-th row represents the projection of all the cubes in the front view such as (x,y,?)

.

Following input a 0/1 matrix with my

lines and mz

columns representing the side view, and the z

-th column of the y

-th row represents the projections of all the cubes in the side view such as (?,y,z)

.

Following input a 0/1 matrix with mz

lines and mx

columns representing the top view, and the x

-th column of the z

-th row represents the projection of all the cubes of the top view such as (x,?,z)

.

The '?

' in the above coordinates represents any integer. Numbers in the same line are separated by spaces. For more detailed input information, please see the sample

Output

For each test case:

The first line of output should contain an integer, representing the volume of the part determined by the three views. If the determined part is not unique, find the largest of all possible parts.

Keke's teacher promises that there is at least one part that satisfies the input.

Sample Input

5 6 4

1 1 1 1 1 1

0 0 0 1 0 1

0 0 0 1 0 1

0 0 0 0 0 1

0 0 0 0 0 1

0 1 1 0

1 0 0 1

0 0 0 1

0 0 0 1

0 0 0 1

1 1 1 1

1 0 0 0 0

1 0 0 0 0

1 0 0 0 0

1 1 1 1 1

Sample Output

17

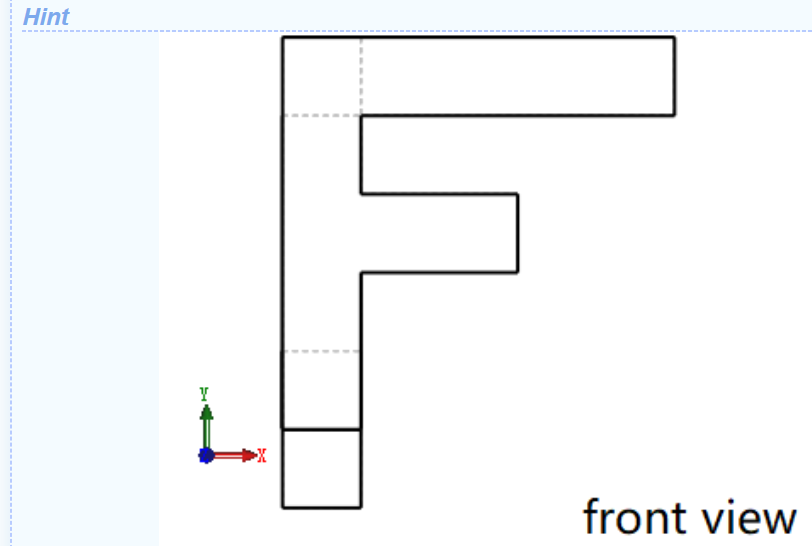
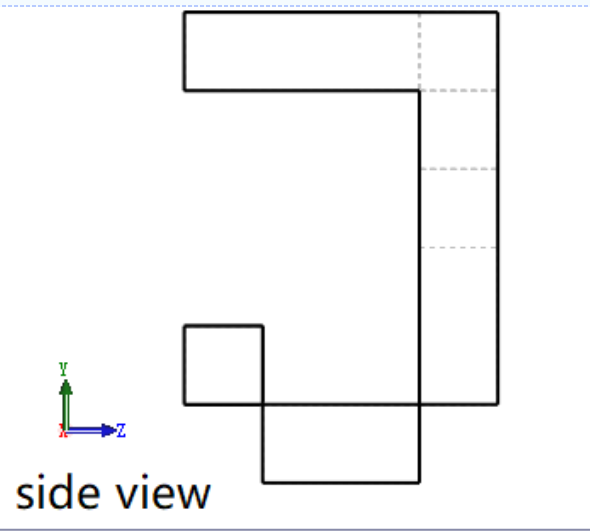
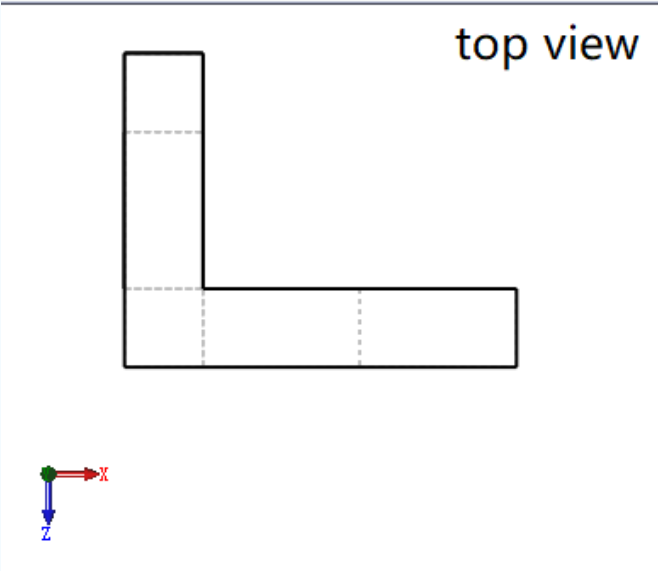
解题思路：这道题就是给你三视图，叫你求体积；

（1）首先题给的这个正视图和侧视图不是真实图的正视图和侧视图，所以应该翻转一下；

 

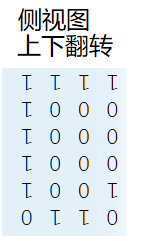
（2）此时就暴力的枚举每个小块，如果都为1，那么就ans++；这样不会出现重复的情况；

代码如下：

 #include<iostream>
 #include<stdio.h>
 using namespace std;
 
 int m , n , k;
 int x[][];
 int y[][];
 int z[][];
 int tpx[][];
 int tpy[][];
 int ans = ;
 int main()
 {
     while(scanf("%d%d%d",&m,&n,&k)!=EOF)
     {
         ans = ;
         for(int i =  ; i <= m ; i++)
         {
             for(int j =  ; j <= n ; j++)
             {
                 cin>>x[i][j];
             }
         }
         for(int i =  ; i <= n ;i++)
         {
             for(int j =  ;j <= k ;j++)
             {
                 cin>>y[i][j];
             }
         }
         for(int i =  ; i <= k ; i ++)
         {
             for(int j =  ; j <= m ;j++)
             {
                 cin>>z[i][j];
             }
         }
 
         for(int i =  ; i <= n ; i++)
         {
             for(int j =  ; j <= m ;j++)
             {
              tpx[i][j] = x[j][n-i+] ;      //向左翻转
             }
         }
 
         for(int i =  ; i <= n ;i++)
         {
             for(int j =  ;j <= k ;j++)
             {
                 tpy[i][j] = y[n-i+][j];  //上下翻转
             }
         }
         for(int i =  ; i <= m ;i++)
         {
             for(int j =  ; j <= n ;j++)
             {
                 for(int l =  ; l <= k ;l++)
                 {
                     if(tpx[j][i]==&&z[l][i]==&&tpy[j][l]==)
                     {
                         ans++;
                     }
                 }
             }
         }
 
         cout<<ans<<endl;
 
     }
 }