清北学堂（2019 4 30 ） part 3

今天总的讲些算法，会了的话...看上去好厉害的样子：

1.老朋友动态规划DP：

　　DP重点：

　　1.边界条件，开头不需处理的数据，比如斐波那契数列中的第一二项

　　2.转移方程，后面的项需要根据前面几项求出自身值的方程（等式）

　　套路：

　　1.定状态，

　　2.写方程，

　　3.敲代码

　　三种用法：

　　1.顺着推，

　　2.倒着推，

　　3.记忆化搜索，

　　举个栗子——斐波那契：

　　1.倒着推：比较简单，只写方程：f[n]=f[n-1]+f[n-2]

　　2.顺着推：代码

#include<bits/stdc++.h>
using namespace std;
int n;
int f[];
int main(){
    scanf("%d",&n);
    f[]=;
    f[]=;
    for(int i=;i<n;i++){
        f[i+]+=f[i];
        f[i+]+=f[i];
    }
    cout<<f[n]<<endl;
    return ;
}

中间核心部分思想在于最新一项去更新后项，因为由递归公式可得当前f[a]只对f[a+1],f[a+1]产生贡献，而倒着推思想在于用已经推过的值去更新最新一项。

　　3.记忆化搜索：代码：

#include<bits/stdc++.h>
using namespace std;
int f[];
bool vis[];       //用这个bool数组记录是否推过
inline int dfs(int n){
    if(n==) return ;
    if(n==) return ;
    if(vis[n]) return f[n];
    f[n]=dfs(n-)+dfs(n-);
    return f[n];
}
int n;
int main(){
    scanf("%d",&n);
    printf("%d\n",dfs(n));
    return ;
}

　　听说记搜能做出来的动规题，前两种一定能做出来...

　　分类：

　　1.数位dp

　　按照十进制每一位dp，自己写的代码（用动规思想写出的伪高精...）：

#include<bits/stdc++.h>
using namespace std;
int xn[],xm[];
int n,m;
int v[];
int main(){
    scanf("%d%d",&m,&n);
    int tn=,tm=;
    while(n>){
        xn[tn++]=n%;
        n/=;
    }
    while(m>){
        xm[tm++]=m%;
        m/=;
    }
    for(int i=tn-;i>=;i--)
        v[i]=v[i+]*+xn[i]-xm[i];
    printf("%d",v[]+);
    return ;
}

　　大佬的：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int f[][],z[],l,r;
int solve(int x){
    int n=;
    while(x){
        z[n]=x%;
        x/=;
        n++;
    }//存一下x的十进制表示
    n--;
    memset(f,,sizeof(f));//要做两个动态规划
    f[n+][]=;
    for(int i=n;i>=;i--)
        for(int j=;j<=;++j){
            if(j==){
                for(int k=;k<=;++k)
                    f[i][]+=f[i+][j];
            }
            else{
                for(int k=;k<=z[i];++k){
                    if(k==z[i]) f[i][]+=f[i+][j];
                    else f[i][]+=f[i+][j];
                }
            }
        }
    return f[][]+f[][];
}

int main(){
    cin>>l>>r;
    cout<<solve(r)-solve(l-)<<endl;
    return ;
}

主要思想是分类讨论，讨论每次处理位数是否相等

　　2.树形dp

　　例题：求n个节点的树有几个节点（exm？！）
　　我其实想用前向星遍历求结果来着，还是练练dp吧，

　　主要思想：

　　根据子树考虑

　　每个叶节点的子树节点个数为1，非叶节点的为所有子树的节点数+1（自身）

　　伪代码：

inline void dfs(int p){
    for(int i=tail[p];i;i=ed[i].next){
        dfs(ed[i].to);
        f[p]+=f[ed[i].to];
    }
    f[p]++;
}

　　大概正确吧...

　　树的直径：

　　给定一棵树，树中每条边都有一个权值，树中两点之间的距离定义为连接两点的路径边权之和。树中最远的两个节点之间的距离被称为树的直径，连接这两点的           路径被称为树的最长链。后者通常也可称为直径，即直径是一个数值概念，也可代指一条路径

　　现给一棵树，求其直径

　　思路：设f[p][0]为p点的最长路，f[p][1]为p点的次长路，分别保存。

　　需根据子树推导，对每个节点进行讨论，对于叶节点，其没有子树，故无法进行讨论，对于其他节点，则讨论其子树，寻找每个子节点的最长路及次长路，然后　       按照方程取:

　　f[p(当前节点)][0]=max(f[p1(子节点1)][0]，f[p2][0],f[p3][0],..........,f[pn][0])+1

　　f[p(当前节点)][1]=max(f[p1(子节点1)][0]，f[p2][0],f[p3][0],.....(加特判不算上一步中取到的点).....,f[pn][0])+1  //因为要去最长路径，所以显然要取最长路径，而不是         次长路，此处容易误认为次长路需从次长路中选。

　　每次处理时用一个变量“sum”取max来维护路长总和，以保证结果一定是最长最优，毕竟难免出现以下这种鬼图的存在...（绘图网站：？？？）

　　所以根节点并不一定是最长路径（直径）经过的点，所以要对每个点进行处理，万一直径的根节点在哪个深山老林里...

　　3.状压dp（听说是最难的）

　　一般空间O(n²*2ⁿ)

　　时间O(2ⁿ*n)

　　一般接受n<=20.

　　（顺便说一下：n<=1000,O(n²)）

　　（n<=100,O(n³)）

　　（n<=10⁵,O（n log n））

　　（n<=10⁶,O(n)）

　　（n<=12,不要考虑复杂度了上暴搜吧）

　　TSP问题：

　　平面上有n个点，问把每个点都走一次的最短路径，并且只能为链，不能为树（更不能是图），如下：

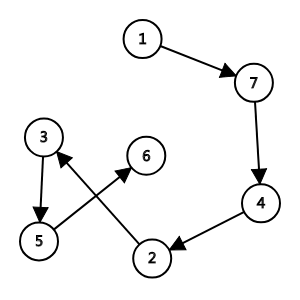
　　状压（状态压缩），用一个数表示一个集合，比如表示上图的路径

　　用二进制实现，如下：

　　对于7 6 5 4 3 2 1，保存路径状态为1 4 6

　　即为0 1 0 1 0 0 1，

　　因每个元素对于一个状态来说只有在其中或不在两种状态，可用1与0表示，而对于不同元素

　　其对应二进制位有独特的位置与权值，所以每一种状态都有唯一的十进制数与其对应

　　其状态用f[s][i]表示，s为路径压缩结果，即已经走过的点的集合对应十进制数，j为当前停留点

　　

　　4.区间dp

　　从区间中枚举断点，合并左右，找最优方案

　　例题：

　　合并石子

　　代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=,inf=0x7fffffff/;
int f1[maxn][maxn],f2[maxn][maxn];
int a[maxn],sum[maxn],n,ans1,ans2;
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
        scanf("%d",&a[i]);
        a[i+n]=a[i];
    }
    for(int i=;i<=n*;i++){
        sum[i]=sum[i-]+a[i];
        f2[i][i]=;
        f1[i][i]=;
    }
    for(int l=;l<=n;l++){
        for(int i=;i<=*n-l+;i++){
            int j=i+l-;
            f1[i][j]=inf;
            f2[i][j]=;
            for(int k=i;k<j;k++){
                f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+][j]);
                f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+][j]);
            }
            f1[i][j]+=sum[j]-sum[i-];
            f2[i][j]+=sum[j]-sum[i-];
        }
        ans1=inf;
        ans2=;
        for(int i=;i<=n;i++){
            ans1=min(ans1,f1[i][i+n-]);
            ans2=max(ans2,f2[i][i+n-]);
        }
    }
    cout<<ans1<<endl<<ans2;
    return ;
}

　　5.其他（没有套路，只能自己推转移方程）

　　肥肠常烤非常常考

　　例题：数字三角形（终于有道做过的了QAQ）

　　代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>          //怀念不用万用文件头的日子
using namespace std;
int n;
int v[][];
int ans=;
int main(){
    cin>>n;
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            cin>>v[i][j];
    for(int i=;i<=n;i++)
        for(int j=;j<=i;j++)
            v[i][j]=max(v[i-][j-],v[i-][j])+v[i][j];   //因为每项只会“被”左上一项或上面一项产生贡献，只考虑那两项
    for(int i=;i<=n;i++)
        ans=max(ans,v[n][i]);
    cout<<ans;
    return ;
}

　　例题*改

　　对于每项v[i][j]%m，求其最大

　　多开一个维度，[k]，k表示%m剩下的值，dp方程如下：

　　if(f[i-1][j-1][(k-a[i][j])%m]||f[i-1][j][(k-a[i][j])%m])

　　　　f[i][j][k]=true;      //这里f数组为bool，结果直接输出k