[Luogu4631][APIO2018] Circle selection 选圆圈

Luogu

题目描述

在平面上，有 \(n\) 个圆，记为 \(c_1, c_2,...,c_n\) 。我们尝试对这些圆运行这个算法：

\(1\)、找到这些圆中半径最大的。如果有多个半径最大的圆，选择编号最小的。记为\(c_i\)。

\(2\)、删除\(c_i\)及与其有交集的所有圆。两个圆有交集当且仅当平面上存在一个点，这个点同时在这两个圆的圆周上或圆内。（原文直译：如果平面上存在一个点被这两个圆所包含，我们称这两个圆有交集。一个点被一个圆包含，当且仅当它位于圆内或圆周上。）

\(3\)、重复上面两个步骤直到所有的圆都被删除。

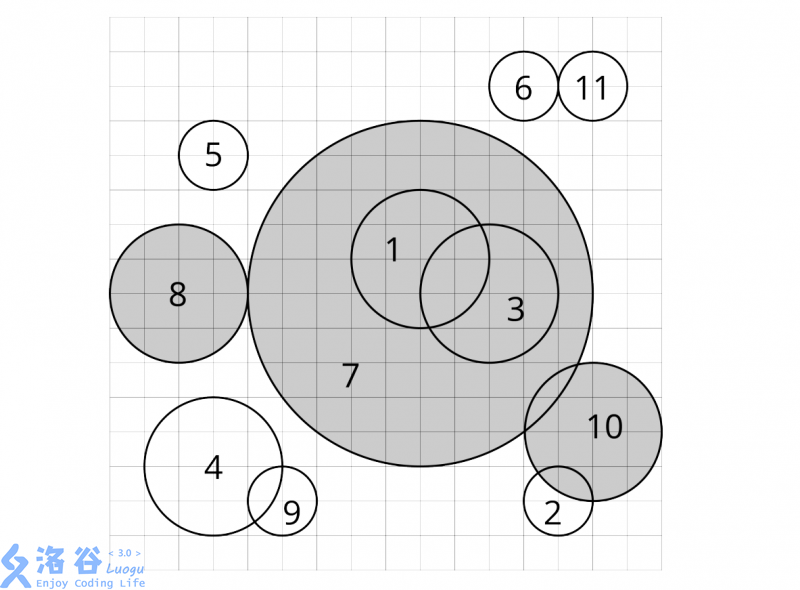
当\(c_i\)被删除时，若循环中第\(1\)步选择的圆是\(c_j\)，我们说\(c_i\)被\(c_j\)删除。对于每个圆，求出它是被哪一个圆删除的。

sol

正解我不会啊qaq

\(kdt\)乱搞就过去了？

就是每个节点维护一下这些圆所在的最小矩形，查的时候如果一个圆被删掉了那就在它的父亲节点里面清除其贡献。

记得把坐标转个角度不会被卡。

code

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
int gi(){
	int x=0,w=1;char ch=getchar();
	while ((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
	if (ch=='-') w=0,ch=getchar();
	while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
	return w?x:-x;
}
#define cmin(a,b) (a>b?a=b:a)
#define cmax(a,b) (a<b?a=b:a)
const int N = 3e5+5;
const double inf = 1e20;
const double eps = 1e-3;
const double alpha = acos(-1)/5;
int n,root,ans[N];
struct Cir{double x,y,r;int id;}a[N],cur;
struct kdtree{
	Cir c;
	double x1,y1,x2,y2;
	int ls,rs;
}t[N];
bool cmpx(Cir i,Cir j){
	return i.x<j.x;
}
bool cmpy(Cir i,Cir j){
	return i.y<j.y;
}
bool cmpr(Cir i,Cir j){
	if (i.r==j.r) return i.id<j.id;
	return i.r>j.r;
}
void mt(int x,int y){
	cmin(t[x].x1,t[y].x1);cmax(t[x].x2,t[y].x2);
	cmin(t[x].y1,t[y].y1);cmax(t[x].y2,t[y].y2);
}
void pushup(int o){
	if (!ans[t[o].c.id]){
		t[o].x1=t[o].c.x-t[o].c.r;
		t[o].x2=t[o].c.x+t[o].c.r;
		t[o].y1=t[o].c.y-t[o].c.r;
		t[o].y2=t[o].c.y+t[o].c.r;
	}else
		t[o].x1=t[o].y1=inf,t[o].x2=t[o].y2=-inf;
	if (t[o].ls) mt(o,t[o].ls);
	if (t[o].rs) mt(o,t[o].rs);
}
int build(int l,int r,int op){
	int o=l+r>>1;
	nth_element(a+l,a+o,a+r+1,op?cmpx:cmpy);
	t[o].c=a[o];
	if (l<o) t[o].ls=build(l,o-1,op^1);
	if (o<r) t[o].rs=build(o+1,r,op^1);
	pushup(o);
	return o;
}
bool out(int o){
	return t[o].x1>cur.x+cur.r+eps||t[o].x2+eps<cur.x-cur.r||t[o].y1>cur.y+cur.r+eps||t[o].y2+eps<cur.y-cur.r;
}
bool check(Cir o){
	return (o.x-cur.x)*(o.x-cur.x)+(o.y-cur.y)*(o.y-cur.y)<=(o.r+cur.r)*(o.r+cur.r)+eps;
}
void query(int o){
	if (out(o)) return;
	if (!ans[t[o].c.id]&&check(t[o].c)) ans[t[o].c.id]=cur.id;
	if (t[o].ls) query(t[o].ls);
	if (t[o].rs) query(t[o].rs);
	pushup(o);
}
int main(){
	n=gi();
	for (int i=1;i<=n;++i){
		int x=gi(),y=gi(),r=gi();
		a[i]=(Cir){x*cos(alpha)+y*sin(alpha),y*cos(alpha)-x*sin(alpha),r,i};
	}
	root=build(1,n,0);
	sort(a+1,a+n+1,cmpr);
	for (int i=1;i<=n;++i)
		if (!ans[a[i].id]) cur=a[i],query(root);
	for (int i=1;i<=n;++i) printf("%d ",ans[i]);
	puts("");return 0;
}