平衡二叉树之RB树

RB树（红黑树）并不追求“完全平衡”——它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能。由于它的设计，任何不平衡都会在三次旋转之内解决。典型的用途是实现关联数组（如C++中的map和set）

只有满足一下性质的树，我们才称之为红黑树：

1）每个结点要么是红的，要么是黑的。

2）根结点是黑的。

3）每个叶结点，即空结点是黑的。

4）如果一个结点是红的，那么它的俩个儿子都是黑的。

5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

红黑树的优点：可以在O(logn)时间内做查找，插入和删除，因为红黑树的高度不会超过2lg(n+1)-->2是因为某一侧子树可能没有红节点，而另一侧正好是红黑每行交错

RB树的插入

只要插入的不是根节点，新插入的节点为红色（这样不会违背性质5），那么只可能违背的是性质4。

情况1：插入的结点的父结点是黑色。
此时不会违反性质4，什么也不用做。这也是2log(n+1)中1的由来。

情况2：当前结点的父结点是红色且祖父结点的另一个子结点（叔叔结点）是红色。
此时父结点的父结点一定存在，否则插入前就已不是红黑树。

对策：将当前节点的父节点和叔叔节点涂黑，祖父结点涂红，把当前结点指向祖父节点，从新的当前节点重新开始算法。

Example：插入4

变化后

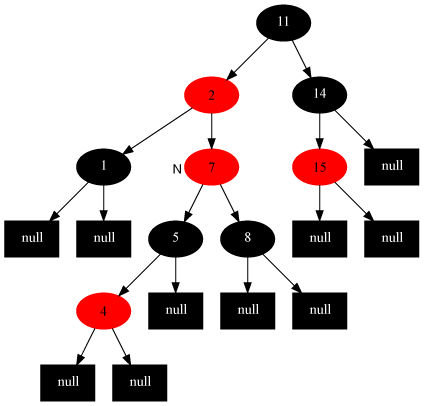
情况3：当前节点的父节点是红色,叔叔节点是黑色，当前节点是其父节点的右子
对策：当前节点的父节点作为新的当前节点，以新当前节点为支点左旋（本文只讨论左子树情况，由于对称性，右子树情况类似）。（右子树过长，左旋到左子树）
Example：当前节点为7

变化后：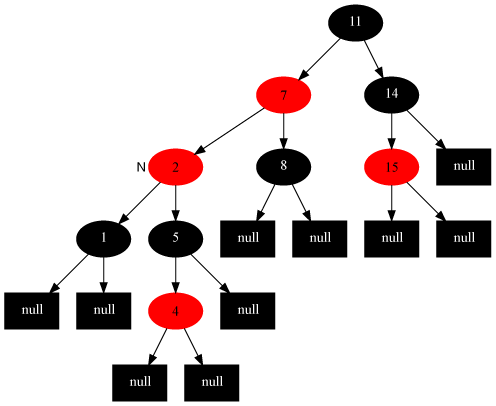

情况4：当前节点的父节点是红色,叔叔节点是黑色，当前节点是其父节点的左子
对策：父节点变为黑色，祖父节点变为红色，在祖父节点为支点右旋（左子树过长，右旋到祖父节点的右子树）

Example: 当前节点为2

变化后

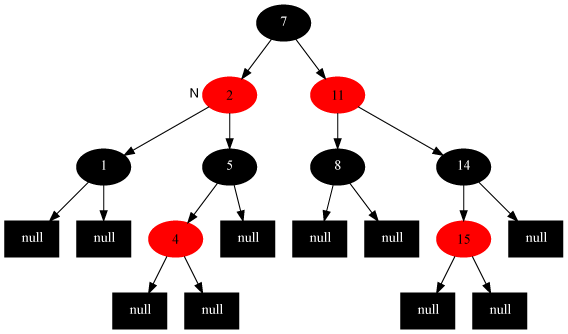
删除操作 （最早的当前节点为待删除的节点）

情况1：当前节点是红色
    对策：直接把当前节点染成黑色，结束。

情况2：当前节点是黑色，且兄弟节点为红色(此时父节点和兄弟节点的子节点必须为黑)。
    对策：把父节点染成红色，把兄弟结点染成黑色，然后，针对父节点做一次左旋。此变换后原红黑树性质5不变，而把问题转化为兄弟节点为黑色的情况。（左子树变短，左旋）

Example: 当前节点为A

变化后

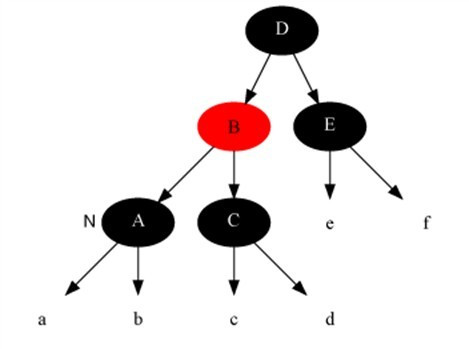
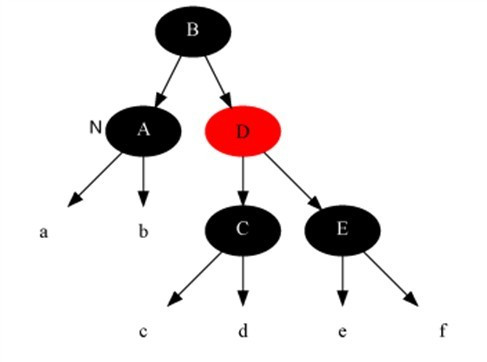
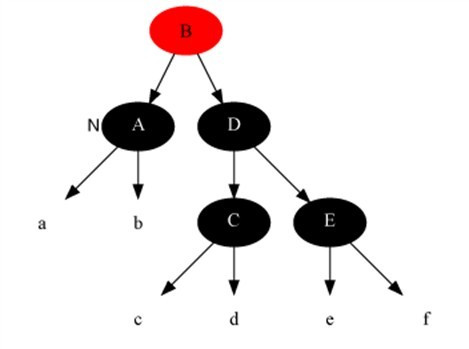
情况3：当前节点是黑色，且兄弟是黑色，且兄弟节点的两个子节点全为黑色。
      解法：把兄弟节点中染红，把父节点当成新的当前节点，重新进入算法。（此变换后性质5不变）

Example: 当前节点为A

变化后

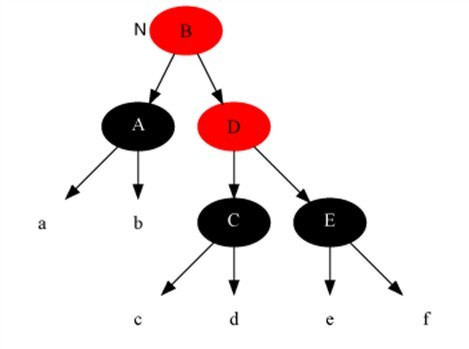
情况4：当前节点颜色是黑色，兄弟节点是黑色，兄弟的左子是红色，右子是黑色。
    对策：把兄弟结点染红，兄弟左子节点染黑，之后再在兄弟节点为支点解右旋，之后重新进入算法。此是把当前的情况转化为情况5，而性质5得以保持。

Example：当前节点为A

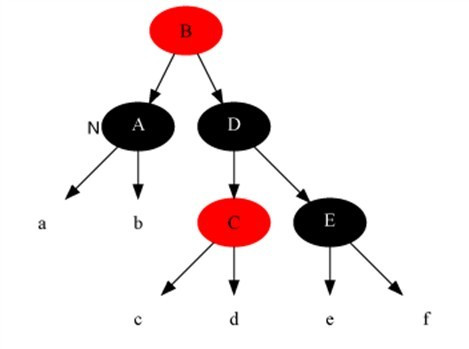
变化后

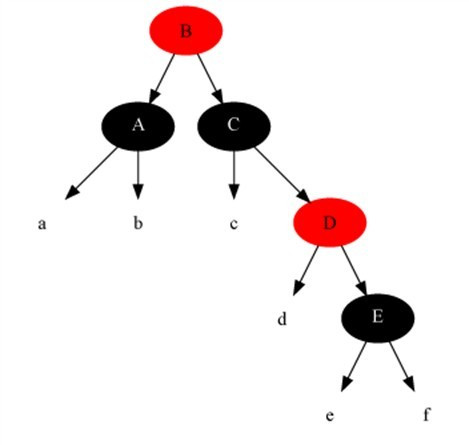
情况5：当前节点颜色是黑色，它的兄弟节点是黑色，但是兄弟节点的右子是红色，兄弟节点左子的颜色任意。

对策：把兄弟节点染成当前节点父节点的颜色，把当前节点父节点染成黑色，兄弟节点右子染成黑色，之后以当前节点的父节点为支点进行左旋，此时算法结束，红黑树所有性质调整正确。

Example：当前节点A

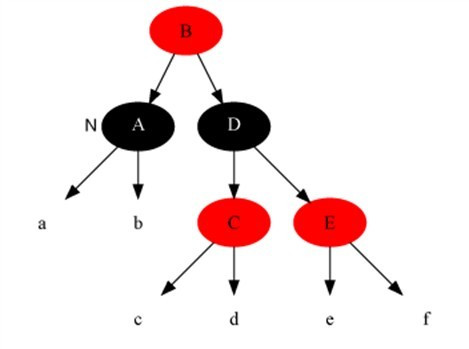
变化后