day40 数据结构-算法（二）

什么是数据结构？

• 简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。
• 比如：列表、集合与字典等都是一种数据结构。
• N.Wirth: “程序=数据结构+算法”

列表

• 列表：在其他编程语言中称为“数组”，是一种基本的数据结构类型。
• 关于列表的问题：
  • 列表中元素使如何存储的？
  • 列表提供了哪些基本的操作？
  • 这些操作的时间复杂度是多少？
• 列表与可变对象*

栈

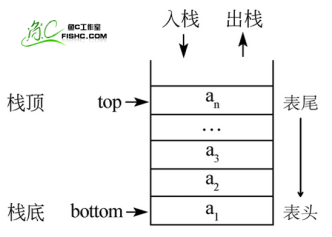
• 栈(Stack)是一个数据集合，可以理解为只能在一端进行插入或删除操作的列表。
• 栈的特点：后进先出（last-in, first-out）
• 栈的概念：
  • 栈顶
  • 栈底
• 栈的基本操作：
  • 进栈（压栈）：push
  • 出栈：pop
  • 取栈顶：gettop

栈的Python实现

• 不需要自己定义，使用列表结构即可。
  • 进栈函数：append
  • 出栈函数：pop
  • 查看栈顶函数：li[-1]

栈的应用——括号匹配问题

• 括号匹配问题：给一个字符串，其中包含小括号、中括号、大括号，求该字符串中的括号是否匹配。
• 例如：
  • ()()[]{} 匹配
  • ([{()}]) 匹配
  • []( 不匹配
  • [(]) 不匹配

括号匹配问题——实现

 def check_kuohao(s):
     stack = []
     for char in s:
         if char in {'(', '[', '{'}:
             stack.append(char)
         elif char == ')':
             if len(stack) > 0 and stack[-1] == '(':
                 stack.pop()
             else:
                 return False
         elif char == ']':
             if len(stack) > 0 and stack[-1] == '[':
                 stack.pop()
             else:
                 return False
         elif char == '}':
             if len(stack) > 0 and stack[-1] == '{':
                 stack.pop()
             else:
                 return False
     if len(stack) == 0:
         return True
     else:
         return False

栈的应用——迷宫问题

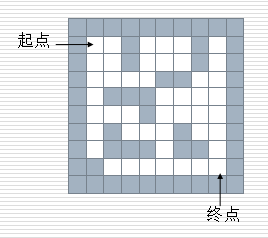
给一个二维列表，表示迷宫（0表示通道，1表示围墙）。给出算法，求一条走出迷宫的路径。

maze = [ [1,1,1,1,1,1,1,1,1,1],

　　　　[1,0,0,1,0,0,0,1,0,1],

　　　　[1,0,0,1,0,0,0,1,0,1],

　　　　 [1,0,0,0,0,1,1,0,0,1],

　　　　[1,0,1,1,1,0,0,0,0,1],

　　　　 [1,0,0,0,1,0,0,0,0,1],

　　　　[1,0,1,0,0,0,1,0,0,1],

　　　　[1,0,1,1,1,0,1,1,0,1],

　　　　[1,1,0,0,0,0,0,0,0,1],

　　　　[1,1,1,1,1,1,1,1,1,1]

　　　　]

解决思路

• 在一个迷宫节点(x,y)上，可以进行四个方向的探查：maze[x-1][y], maze[x+1][y], maze[x][y-1], maze[x][y+1]
• 思路：从一个节点开始，任意找下一个能走的点，当找不到能走的点时，退回上一个点寻找是否有其他方向的点。
• 方法：创建一个空栈，首先将入口位置进栈。当栈不空时循环：获取栈顶元素，寻找下一个可走的相邻方块，如果找不到可走的相邻方块，说明当前位置是死胡同，进行回溯（就是讲当前位置出栈，看前面的点是否还有别的出路）

迷宫问题——栈实现

 dirs = [lambda x, y: (x + 1, y), lambda x, y: (x - 1, y),
 lambda x, y: (x, y - 1), lambda x, y: (x, y + 1)]
 def mgpath(x1, y1, x2, y2):
     stack = []
     stack.append((x1, y1))
     while len(stack) > 0:  # 栈不空时循环
         curNode = stack[-1]  # 查看栈顶元素
         if curNode[0] == x2 and curNode[1]:
             # 到达终点
             for p in stack:
                 print(p)
             break
         for dir in dirs:
             nextNode = dir(*curNode)
             if mg[nextNode[0]][nextNode[1]] == 0:  # 找到了下一个方块
                 stack.append(nextNode)
                 mg[nextNode[0]][nextNode[1]] = -1  # 标记为已经走过，防止死循环
                 break
         else:
             mg[curNode[0]][curNode[1]] = -1  # 死路一条
             stack.pop()
         return False

队列

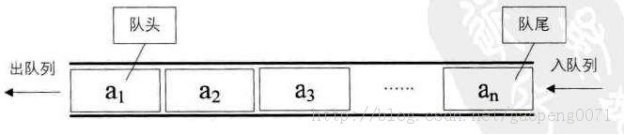
• 队列(Queue)是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。
• 进行插入的一端称为队尾(rear)，插入动作称为进队或入队
• 进行删除的一端称为队头(front)，删除动作称为出队
• 队列的性质：先进先出(First-in, First-out)
• 双向队列：队列的两端都允许进行进队和出队操作。

队列的实现

• 队列能否简单用列表实现？为什么？
• 使用方法：from collections import deque
  • 创建队列：queue = deque(li)
  • 进队：append
  • 出队：popleft
  • 双向队列队首进队：appendleft
  • 双向队列队尾进队：pop

队列的实现原理

• 初步设想：列表+两个下标指针
• 创建一个列表和两个变量，front变量指向队首，rear变量指向队尾。初始时，front和rear都为0。
• 进队操作：元素写到li[rear]的位置，rear自增1。
• 出队操作：返回li[front]的元素，front自减1。
• 这种实现的问题？
• 

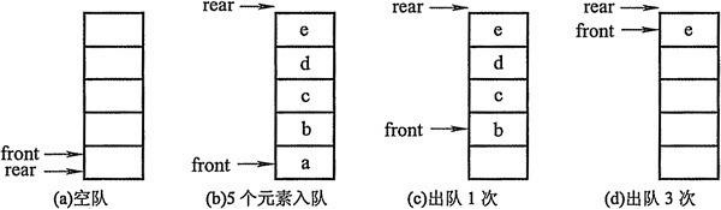
队列的实现原理——环形队列

• 改进方案：将列表首尾逻辑上连接起来。

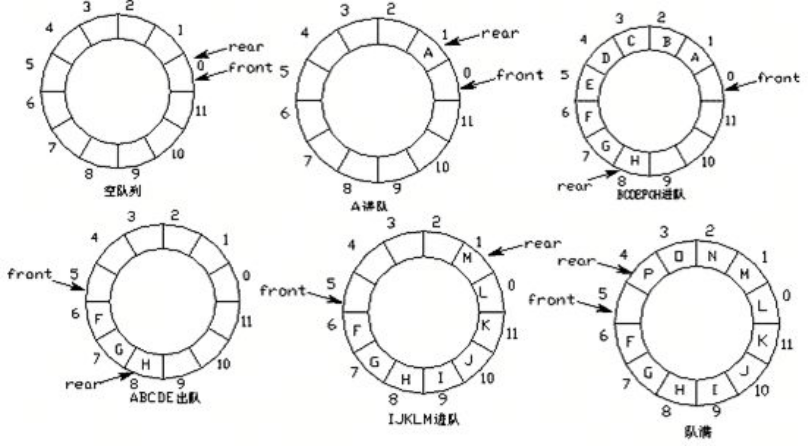
队列的实现原理——环形队列

• 环形队列：当队尾指针front == Maxsize + 1时，再前进一个位置就自动到0。
  • 实现方式：求余数运算
  • 队首指针前进1：front = (front + 1) % MaxSize
  • 队尾指针前进1：rear = (rear + 1) % MaxSize
  • 队空条件：rear == front
  • 队满条件：(rear + 1) % MaxSize == front

队列的应用——迷宫问题

• 思路：从一个节点开始，寻找所有下面能继续走的点。继续寻找，直到找到出口。
• 方法：创建一个空队列，将起点位置进队。在队列不为空时循环：出队一次。如果当前位置为出口，则结束算法；否则找出当前方块的4个相邻方块中可走的方块，全部进队。

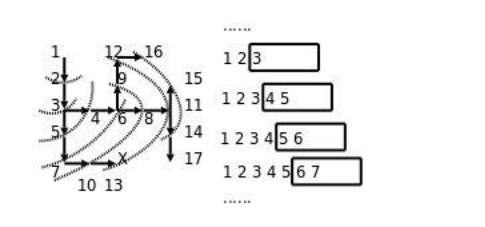
迷宫问题——队列实现

 def mgpath(x1, y1, x2, y2):
     queue = deque()
     path = []
     queue.append((x1, y1, -1))
     while len(queue) > 0:
         curNode = queue.popleft()
         path.append(curNode)
         if curNode[0] == x2 and curNode[1] == y2:
             #到达终点
             print(path)
             return True
         for dir in dirs:
             nextNode = dir(curNode[0], curNode[1])
             if mg[nextNode[0]][nextNode[1]] == 0:  # 找到下一个方块
                 queue.append((*nextNode, len(path) - 1))
                 mg[nextNode[0]][nextNode[1]] = -1  # 标记为已经走过
     return False

链表

链表中每一个元素都是一个对象，每个对象称为一个节点，包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接，最终串联成一个链表。

节点定义：

class Node(object):
    def __init__(self, item):
        self.item = item
        self.next = None

头结点

链表的遍历

• 遍历链表：

• def traversal(head):
      curNode = head  # 临时用指针
      while curNode is not None:
          print(curNode.data)
          curNode = curNode.next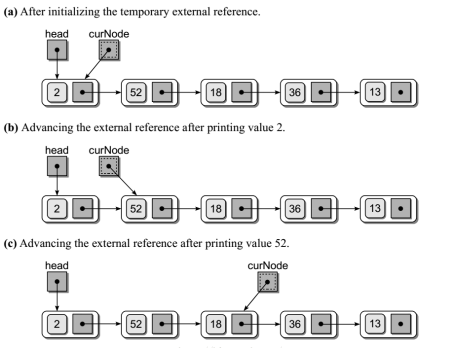

  

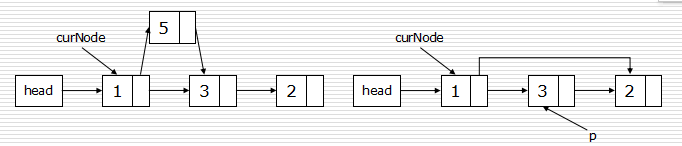
链表节点的插入和删除

• 插入：
  • p.next = curNode.next
  • curNode.next = p
• 删除：
  • p = curNode.next
  • curNode.next = curNode.next.next
  • del p

建立链表

• 头插法：

•  def createLinkListF(li):
       l = Node()
       for num in li:
           s = Node(num)
           s.next = l.next
           l.next = s
       return l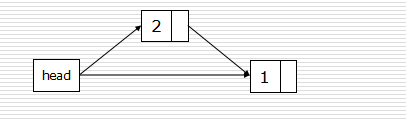

  

• 尾插法：

•  def createLinkListR(li):
       l = Node()
       r = l       #r指向尾节点
       for num in li:
           s = Node(num)
           r.next = s
           r = s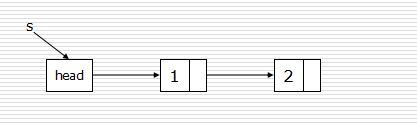

  

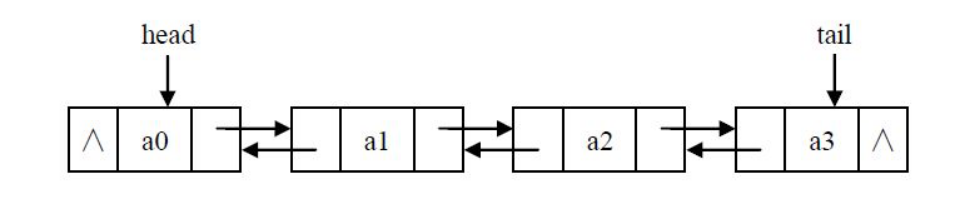
双链表

双链表中每个节点有两个指针：一个指向后面节点、一个指向前面节点。

节点定义：

 class Node(object):
     def __init__(self, item=None):
         self.item = item
         self.next = None
         self.prior = None

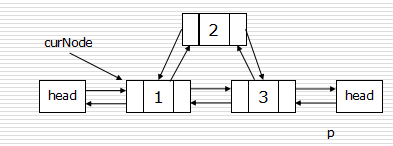
双链表节点的插入和删除

• 插入：
  • p.next = curNode.next
  • curNode.next.prior = p
  • p.prior = curNode
  • curNode.next = p
• 删除：
  • p = curNode.next
  • curNode.next = p.next
  • p.next.prior = curNode
  • del p

建立双链表

• 尾插法：

•  def createLinkListR(li):
       l = Node()
       r = l
       for num in li:
           s = Node(num)
           r.next = s
           s.prior = r
           r = s
       return l, r

链表-分析

• 列表与链表
  • 按元素值查找
  • 按下标查找
  • 在某元素后插入
  • 删除某元素

Python中的集合与字典（了解）

• 哈希表查找
• 哈希表（Hash Table，又称为散列表），是一种线性表的存储结构。通过把每个对象的关键字k作为自变量，通过一个哈希函数h(k)，将k映射到下标h(k)处，并将该对象存储在这个位置。
• 例如：数据集合{1,6,7,9}，假设存在哈希函数h(x)使得h(1) = 0, h(6) = 2, h(7) = 4, h(9) = 5，那么这个哈希表被存储为[1,None, 6, None, 7, 9]。
• 当我们查找元素6所在的位置时，通过哈希函数h(x)获得该元素所在的下标（h(6) = 2），因此在2位置即可找到该元素。
• 哈希函数种类有很多，这里不做深入研究。
• 哈希冲突：由于哈希表的下标范围是有限的，而元素关键字的值是接近无限的，因此可能会出现h(102) = 56， h(2003) = 56这种情况。此时，两个元素映射到同一个下标处，造成哈希冲突。

解决哈希冲突：

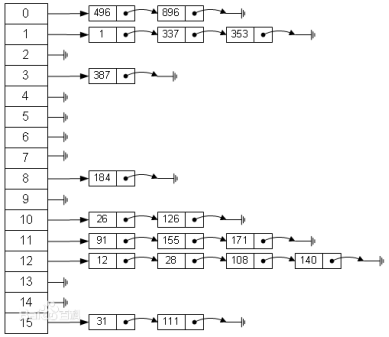
• 拉链法
  • 将所有冲突的元素用链表连接
• 开放寻址法
  • 通过哈希冲突函数得到新的地址

• 在Python中的字典： a = {'name': 'Alex', 'age': 18, 'gender': 'Man'}
• 使用哈希表存储字典，通过哈希函数将字典的键映射为下标。假设h(‘name’) = 3, h(‘age’) = 1, h(‘gender’) = 4，则哈希表存储为[None, 18, None, ’Alex’, ‘Man’]
• 在字典键值对数量不多的情况下，几乎不会发生哈希冲突，此时查找一个元素的时间复杂度为O(1)。