bzoj3143: [Hnoi2013]游走（贪心+高斯消元）

　　考虑让总期望最小，那么就是期望经过次数越多的边贪心地给它越小的编号。

　　怎么求每条边的期望经过次数呢？边不大好算，我们考虑计算每个点的期望经过次数f[x]，那么一条边的期望经过次数就是f[x]/d[x]+f[y]/d[y]，d为度。

　　点的期望经过次数就很好算啦~

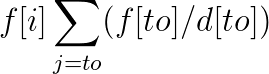
　　注意1一开始已经经过了1次，于是f[1]=sigma(f[to]/d[to)+1，到n之后就结束，所以到n的边的期望次数其实不由n决定，那直接把f[n]设为0，而且到n之后就结束，所有点是不能算从n来的边的，但是f[n]为0，所以就无所谓啦~

　　然后高斯消元，算出边的期望经过次数，期望经过次数越多的边贪心地给它越小的编号就好了。

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
const int maxn=,maxm=,inf=1e9;
struct poi{int too,pre;}e[maxm<<];
int n,m,tot;
int last[maxn],d[maxn],x[maxm],y[maxm];
double ans;
double a[maxn][maxn],f[maxm];
void read(int &k)
{
    int f=;k=;char c=getchar();
    while(c<''||c>'')c=='-'&&(f=-),c=getchar();
    while(c<=''&&c>='')k=k*+c-'',c=getchar();
    k*=f;
}
void add(int x,int y){e[++tot].too=y;e[tot].pre=last[x];last[x]=tot;}
bool gauss()
{
    int to,now=;double x;
    for(int i=;i<=n;i++,now++)
    {
        for(to=now;to<=n;to++)if(fabs(a[to][i])>1e-)break;
        if(to>n)continue;
        if(to!=now)for(int j=;j<=n+;j++)swap(a[now][j],a[to][j]);
        x=a[now][i];for(int j=;j<=n+;j++)a[now][j]/=x;
        for(int j=;j<=n;j++)
        if(now!=j)
        {
            x=a[j][i];
            for(int k=;k<=n+;k++)a[j][k]-=x*a[i][k];
        }
    }
    for(int i=;i<=n;i++)if(a[i][n+]>1e-)return ;
    return ;
}
int main()
{
    read(n);read(m);
    for(int i=;i<=m;i++)
    {
        read(x[i]),read(y[i]);
        add(x[i],y[i]);add(y[i],x[i]);
        d[x[i]]++;d[y[i]]++;
    }
    for(int i=;i<n;i++)
    {
        a[i][i]=1.0;
        for(int j=last[i];j;j=e[j].pre)
        if(e[j].too!=n)a[i][e[j].too]=-1.0/d[e[j].too];
    }
    a[][n+]=1.0;a[n][n]=1.0;
    gauss();for(int i=;i<=m;i++)f[i]=a[x[i]][n+]/d[x[i]]+a[y[i]][n+]/d[y[i]];
    sort(f+,f++m);
    for(int i=;i<=m;i++)ans+=f[i]*(m-i+);
    printf("%.3lf\n",ans);
    return ;
}