JZOJ.5231【NOIP2017模拟8.5】序列问题

Description

 

Input

输入文件名为seq.in。
首先输入n。
接下来输入n个数，描述序列 A。

Output

输出文件名为seq.out。
输出一行一个整数代表答案。

 

Sample Input

7
0 35 40 45 56 65 94

Sample Output

66636

 

Data Constraint

对于30%的数据，n<=5000
对于60%的数据，n<=50000
对于100%的数据，n<=500000,0<=A[i]<=10^9

ST加暴力枚举区间显然过不了，复杂度为O(n²)

考虑分治。对于区间[l,r]，我们可以轻易求得[l,mid]和[mid+1,r]的值，关键在于求$\sum_{x\in[l,\,mid],\,y\in[mid+1,\,r]}f(x,\,y)*g(x,\,y)$

我们可以先枚举右端点r，求得每个点i到mid+1的最大值和最小值max[i]和min[i]，然后从mid开始右往左枚举每一个左端点j，求得min_l,max_l,然后可以求得右端点中从左到右的第一个大于max_l,第一个小于min_l,的位置i，如图所示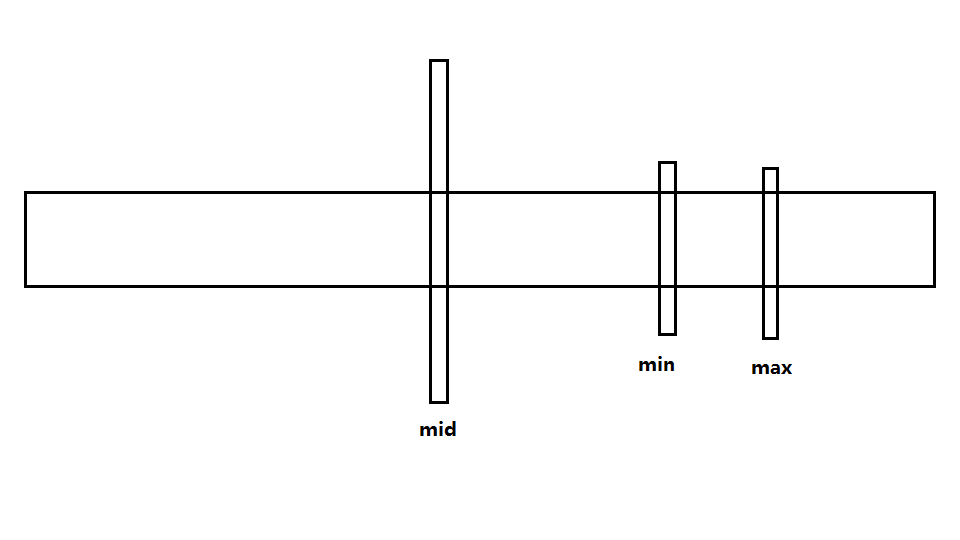（我们假设min的位置在max位置的左边）

这样右边就被分成三段。

对于第一段(mid-min之间)，由于最大值和最小值都是max_l,min_l，所以右端点这一段的值就是min_l*max_l*(min-mid)

对于第二段(min-max之间)，由于最大值是max_l，最小值不定，不过我们可以把max_l提取出来，剩下的就是这段区间min_l的和了，所以我们可以用前缀和维护一下。smin[max-1]-smin[min-1]

对于第三段(max-r之间)，由于最大值最小值都是不定，但是它们都在mid的右边，我们在分治的时候就已经算好了，直接加上去就好了  。 spul[r]-spul[max-1]

min在max右边同理。

 #include<iostream>
 #include<cstdio>
 #define qaq 1000000007
 using namespace std;
 const int N=;
 long long a[N],minn[N],maxx[N],sminn[N],smaxx[N],spul[N],ans;
 int n;
 void fz(long long l,long long r){
     if (r<l) return;
     if (l==r){
         ans=(ans+a[l]*a[r])%qaq;
         return;
     }
     long long mid=(l+r)>>;
     fz(l,mid);
     fz(mid+,r);
     minn[mid]=1e12;
     maxx[mid]=;
     sminn[mid]=;
     smaxx[mid]=;
     spul[mid]=;
     for (int i=mid+;i<=r;i++){
         if (a[i]>maxx[i-]) maxx[i]=a[i];
         else maxx[i]=maxx[i-];
         if (a[i]<minn[i-]) minn[i]=a[i];
         else minn[i]=minn[i-];
         sminn[i]=sminn[i-]+minn[i];
         smaxx[i]=smaxx[i-]+maxx[i];
         spul[i]=(spul[i-]+maxx[i]*minn[i])%qaq;
     }
     long long mi=mid;
     long long ma=mid;
     long long mis=1e12;
     long long mas=;
     for (int i=mid;i>=l;i--){
         if (a[i]<mis) mis=a[i];
         if (a[i]>mas) mas=a[i];
         while ((mi<r)&&(minn[mi+]>=mis)) mi++;
         while ((ma<r)&&(maxx[ma+]<=mas)) ma++;
         if (mi<ma)
         ans=(ans+mis%qaq*mas%qaq*(mi-mid)%qaq+(sminn[ma]-sminn[mi])%qaq*mas%qaq+(spul[r]-spul[ma])%qaq)%qaq;
         else
         ans=(ans+mis%qaq*mas%qaq*(ma-mid)%qaq+(smaxx[mi]-smaxx[ma])%qaq*mis%qaq+(spul[r]-spul[mi])%qaq)%qaq;
     }
 }
 int main(){
     freopen("seq.in","r",stdin);
     freopen("seq.out","w",stdout);
     scanf("%d",&n);
     for (int i=;i<=n;i++)
      scanf("%lld",&a[i]);
     ans=;
     fz(,n);
     printf("%lld\n",ans);
     return ;
 }

神奇的代码

乘的顺序很重要，乘的顺序很重要，乘的顺序很重要！！！（苦悲的ans那里乘的放到后面没有事先%%%就变负数waaaaaaaa了QAQ）