【倍增】LCM QUERY

给一个序列，每次给一个长度l，问长度为l的区间中lcm最小的。

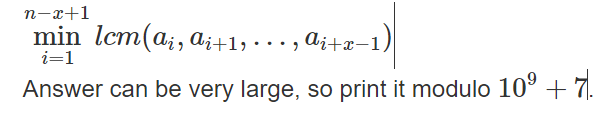
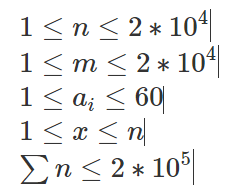
题解：因为ai<60，所以以某个点为左端点的区间的lcm只有最多60种的情况，而且相同的lcm区间的连续的。

所以就想到一个n*60*logn的做法，倍增找出每个点的区间lcm情况，然后修改答案……

1-60的lcm的积大于long long，只能把数拆开，然后比较时用log，结果才用这个数的质因数相乘。

问题在于一开始我对于每个点开个20的数组记录60内第几个质数的个数，这样每次常数就要再乘个20，然后就tle……

优化的方法是位运算，因为只会是2，3，5，7的次幂大于1次，单独记录，其他的只会是0次幂和1次幂。

最后作死的两个小错误：33不是质数……，用ln【60】数组记录log的值然而其中对n取对数……

#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define maxn 40000
#define mm 1000000007
#define LL long long
#define inf 100000000000
#define rep(i,l,r) for(int i=l;i<=r;i++)
#define dow(i,l,r) for(int i=r;i>=l;i--)
using namespace std;

typedef struct {
    int v1;
    double v2;
}Big;
Big tree[maxn*];
double ln[maxn];
int f[maxn][],now;
int n,m,maxln,tot=;
LL ans1[maxn],ans2[maxn];
int pri[]={,,,,
            ,,,,
            ,,,,
            ,,,,
            ,,,,
            ,,,,};

double calc(int x)
{
    double sum=;
    rep(i,,tot)
        if ((x>>i)&)
            sum+=ln[pri[i]];
    dow(i,,)
        if ((x>>i)&) {
            sum+=(i+)*ln[];
            break;
        }
    if ((x>>)&) sum+=*ln[];
    else
    if ((x>>)&) sum+=*ln[];
    else
    if ((x>>)&) sum+=ln[];

    if ((x>>)&) sum+=*ln[];
    else
    if ((x>>)&) sum+=ln[];

    if ((x>>)&) sum+=*ln[];
    else
    if ((x>>)&) sum+=ln[];

    return sum;
}

LL answer(Big x)
{
    LL sum=;
    rep(i,,tot)
        if ((x.v1>>i)&)
            sum=sum*pri[i]%mm;
    dow(i,,)
        if ((x.v1>>i)&) {
            sum=sum*pri[i]%mm;
            break;
        }
    if ((x.v1>>)&) sum=sum*%mm;
    else
    if ((x.v1>>)&) sum=sum*%mm;
    else
    if ((x.v1>>)&) sum=sum*%mm;

    if ((x.v1>>)&) sum=sum*%mm;
    else
    if ((x.v1>>)&) sum=sum*%mm;

    if ((x.v1>>)&) sum=sum*%mm;
    else
    if ((x.v1>>)&) sum=sum*%mm;

    return sum;
}

void build(int x,int l,int r)
{
    tree[x].v2=inf;
    if (l==r) return;
    int mid=(l+r)>>;
    build(x<<,l,mid);
    build(x<<|,mid+,r);
}

void change(int x,int l,int r,int ll,int rr,double z)
{
    if (tree[x].v2<=z) return;
    if (ll<=l && r<=rr) {
        tree[x].v1=now;
        tree[x].v2=z;
        return;
    }
    int mid=(l+r)>>;
    if (ll<=mid) change(x<<,l,mid,ll,rr,z);
    if (rr>mid) change(x<<|,mid+,r,ll,rr,z);
}

Big ask(int x,int l,int r,int y)
{
    if (l==r) return tree[x];
    int mid=(l+r)>>;
    Big more;
    if (y<=mid) more=ask(x<<,l,mid,y);
    else more=ask(x<<|,mid+,r,y);
    if (more.v2<tree[x].v2) return more;
    return tree[x];
}

int main()
{
    rep(i,,maxn-) ln[i]=log(i);
    int tt=;
    while (scanf("%d %d",&n,&m)!=EOF) {
        ++tt;
        rep(i,,n) {
            f[i][]=;
            int k;
            scanf("%d",&k);
            dow(j,,tot)
                if (k%pri[j]==) k/=pri[j],f[i][]+=<<j;
        }
        maxln=floor(ln[n]/ln[])+;
        rep(i,,maxln)
            rep(j,,n+-(<<i))
                f[j][i]=f[j][i-]|f[j+(<<(i-))][i-];
        build(,,n);
        rep(i,,n) {
            int l=i;
            now=;
            while (l<=n) {
            //    printf("!!%d %d\n",now,f[l][0]);
                now=now|f[l][];
                int r=l;
                dow(j,,maxln)
                    if (r-+(<<j)<=n && !(~((~f[r][j])|now)) ) r=r-+(<<j);

                change(,,n,l-i+,r-i+,calc(now));
                l=r+;
            }
        }

        while (m--) {
            int j;
            scanf("%d",&j);
            printf("%lld\n",answer(ask(,,n,j)));
        }
    }
    return ;
}

这种区间答案连续的思想并不是第一次遇见了