BZOJ1043：[HAOI2008]下落的圆盘——题解（配图片）

http://www.lydsy.com/JudgeOnline/problem.php?id=1043

Description

　　有n个圆盘从天而降，后面落下的可以盖住前面的。求最后形成的封闭区域的周长。看下面这副图, 所有的红
色线条的总长度即为所求.

Input

　　第一行为1个整数n,N<=1000
接下来n行每行3个实数,ri,xi,yi,表示下落时第i个圆盘的半径和圆心坐标.

Output

　　最后的周长，保留三位小数

Sample Input

2
1 0 0
1 1 0

Sample Output

10.472

————————————————————————————————

代码借（抄）鉴（袭）于：http://blog.csdn.net/Vmurder/article/details/46564199

首先我们通过枚举判断两圆的关系：后全覆盖先，先全覆盖后，后和先相交，后和先相离。

显然2和4是没有影响的，而1相当于将先圆干掉了（因为它不再对答案有贡献了）

所以重点在3情况上。

我们弧长公式有：L=角（弧度制）*半径（R）。

所以我们可以用弧度制来表示当前圆被覆盖的部分，即可求出弧长。

基本上高中数学知识即可解决，这里配一张图：

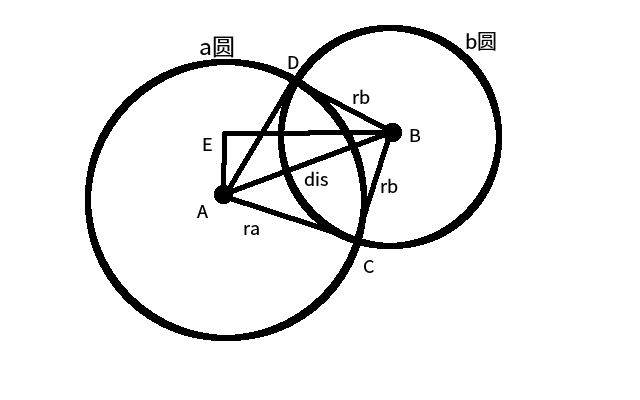
我们这里让a圆覆盖b圆，求b被覆盖的圆心角区间。

我们首先发现图中所有的线段长度都能求出来。

我们设∠EBA为alpha，显然△ADB和△ACB全等，则设∠DBA=∠CBA=beta

那么

alpha=arctan(AE/EB)

beta=arccos((BD*BD+BA*BA-DA*DA)/(2*BD*BA))=arccos((rb*rb+dis*dis-ra*ra)/(2*rb*dis))

//余弦定理

那么∠DBE=alpha-beta，∠EBC=alpha+beta

（这里可以发现我们圆心角的0度被我们定义在了左边，和常识不同请注意）

我们将圆心角控制在[-180度，180度]，所以一旦超过了这个区间我们就要对其进行修改。

修改操作详见gai函数。

#include<cstdio>
#include<queue>
#include<cctype>
#include<cstring>
#include<stack>
#include<cmath>
#include<algorithm>
using namespace std;
typedef double dl;
const int N=;
const dl poi=acos(-1.0);
struct circle{
    dl r;
    dl x;
    dl y;
}p[N];
struct line{
    dl l;
    dl r;
}seg[N][*N];
int n,cnt[N];
bool die[N];
inline dl dis(circle a,circle b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
inline int inc(circle a,circle b){
    dl d=dis(a,b);
    if(a.r+b.r<d)return ;//两圆相离
    if(a.r>b.r&&a.r-b.r>d)return -;//a覆盖b
    if(b.r>a.r&&b.r-a.r>d)return ;//b覆盖a
    return ;//两圆相交
}
inline void getinc(circle a,circle b,dl &i,dl &j){//a覆盖b
    double alpha=atan2((b.y-a.y),(b.x-a.x));
    dl d=dis(a,b);
    double beta=acos((b.r*b.r+d*d-a.r*a.r)/(*b.r*d));
    i=alpha-beta;
    j=alpha+beta;
    return;
}
inline bool gai(line &a){
    if(a.r>poi){
    a.r-=*poi;
    return ;
    }
    if(a.l<-poi){
    a.l+=*poi;
    return ;
    }
    return ;
}
bool cmp(line a,line b){
    return a.l<b.l;
}
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++){
    scanf("%lf%lf%lf",&p[i].r,&p[i].x,&p[i].y);
    for(int j=;j<i;j++){
        if(die[j])continue;
        int k=inc(p[i],p[j]);
        if(!k)continue;
        if(k==-){
        die[j]=;
        continue;
        }
        cnt[j]++;
        getinc(p[i],p[j],seg[j][cnt[j]].l,seg[j][cnt[j]].r);
        if(gai(seg[j][cnt[j]])){
        cnt[j]++;
        seg[j][cnt[j]].l=-poi;
        seg[j][cnt[j]].r=seg[j][cnt[j]-].r;
        seg[j][cnt[j]-].r=poi;
        }
    }
    }
    dl ans=;
    for(int i=;i<=n;i++){
    if(!die[i]){
        dl re=*poi,L,R;
        if(cnt[i]){
        sort(seg[i]+,seg[i]+cnt[i]+,cmp);
        L=seg[i][].l;R=seg[i][].r;
        for(int j=;j<=cnt[i];j++){
            if(seg[i][j].l>R){
            re-=R-L;
            L=seg[i][j].l;
            R=seg[i][j].r;
            }else{
            R=max(R,seg[i][j].r);
            }
        }
        re-=R-L;
        }
        ans+=re*p[i].r;
    }
    }
    printf("%.3lf\n",ans);
    return ;
}