[笔记]KMP算法 - 上（算法详解）

算法详解

KMP 是一种字符串匹配算法，可以在线性的时间复杂度内解决字符串的“模式定位”问题，即：

在字符串 $A$ 中查找字符串 $B$ 出现的所有位置。

我们称 $A$ 为主串，$B$ 为模式串。下文都用 $n$ 表示 $A$ 的长度，$m$ 表示 $B$ 的长度，下标从 $1$ 开始。

初始状态，我们用两个指针 $i,j$ 分别指向 $A$ 和 $B$ 的第 $1$ 位。

KMP 的主过程如下（后面会证明它的正确性）：

如果 $A[i]=B[j]$，则i++，j++。
如果 $A[i]\neq B[j]$：
- 如果 $j>1$，则j=nxt[j-1]+1。
- 如果 $j\le 1$，则i++。

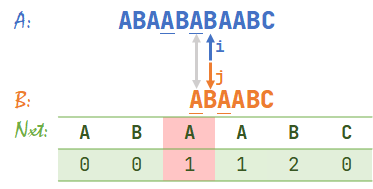
其中，$nxt$ 数组是一个用于表示发生失配后，$j$ 回退到的位置。具体求法待会会说，下面我们用一个例子来理解 $nxt$ 的功能，我将 $nxt$ 数组画在图片的下方了。

初始状态。$i=1,j=1$。
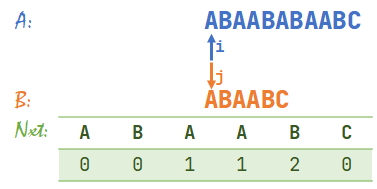
$A[i]=B[j]$，同时右移 $i,j$。$i=2,j=2$。
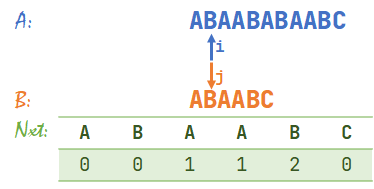
$A[i]=B[j]$，同时右移 $i,j$。$i=3,j=3$。
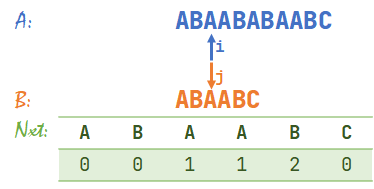
$A[i]=B[j]$，同时右移 $i,j$。$i=4,j=4$。
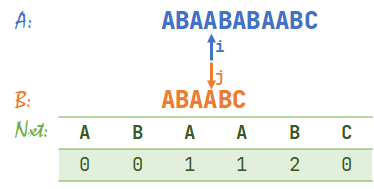
$A[i]=B[j]$，同时右移 $i,j$。$i=5,j=5$。
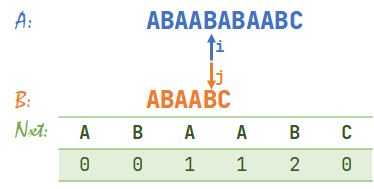
$A[i]=B[j]$，同时右移 $i,j$。$i=6,j=6$。
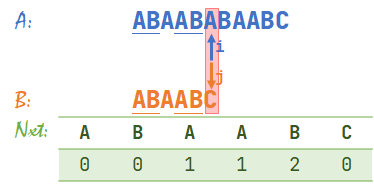
发现 $A[i]\neq B[j]$，于是查表 $nxt[j-1]+1=nxt[5]+1=3$，于是 $j=3$。此时 $i=6$。

可以发现此时灰色箭头指向的两部分是相等的。

进一步来说，从上一张图开始，下划线的部分都是相等的。
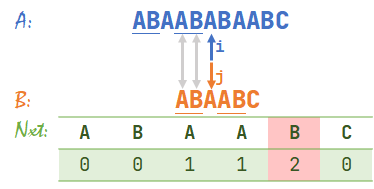
OK我们继续，$A[i]=B[j]$，于是 $i,j$ 同时右移，$i=7,j=4$。
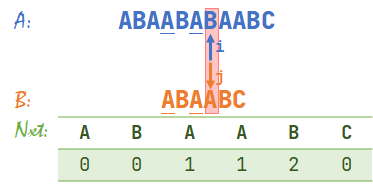
发现 $A[i]\neq B[j]$，查表得 $nxt[3]+1=2$，于是 $j=2$。此时 $i=7$。

我们又发现 $A$ 与 $B$ 的下划线部分重合了，所以仍然可以从重合部分之后开始比较。
然后 $A[i]=B[j]$……就一直比到结束了，就不放图了w。

似乎2.2的情况没有提到呢……其实就是如果第 $1$ 个字符就失配，就i++，这是很自然的。

我们可以把根据上面的过程（KMP 主过程）写出代码（下标从 $1$ 开始）：

i=1,j=1;

while(i<=n){

	if(a[i]==b[j]) i++,j++;

	else if(j>1) j=nxt[j-1]+1;

	else i++;

	if(j==m+1) cout<<i-j+1<<"\n";

	//输出配对的开始位置，理解一下这里

}

可以发现 $i$ 是始终不降的，比起暴力，KMP 通过避免 $i$ 指针的回滚操作，减少了时间开销。

到这里我们已经可以初步理解 $nxt$ 的含义，它是用来帮我们了解发生失配时，$j$ 应该回退到什么位置。

再进一步分析，我们发现：$nxt[x]$，其实就是 $B[1\sim x]$ 这一段的最长公共前后缀长度。

举个例子，YABAPQYABZABAAPYABAPQYABA。这是一个长度为 $25$ 的字符串，那么当它作为 $B$ 时：

$nxt[24]=9$，如你所见，红色部分是 $B[1\sim 24]$ 的公共前后缀，它的长度为 $9$。
$nxt[9]=3$，因为YAB是 $B[1\sim 9]$ 的公共前后缀，它的长度为 $3$。
$nxt[3]=0$，因为 $B[1\sim 3]$ 没有公共前后缀。
$nxt[25]=4$，因为YABA是 $B[1\sim 25]$ 的公共前后缀。

注意：公共前后缀可能有重叠部分，但是一个字符串不能作为它自己的公共前后缀（严格来说，我们把这种前/后缀称作真前/后缀，所以后面都带“真”来称呼了）。

公共真前后缀也可以称为border（不一定是最长），自然一个字符串可能有多个border。

我们规定，$nxt[x]$ 表示的必须是 $B[1\sim x]$ 这一段的最长公共真前后缀长度，这么定义是为了保证正确性，如果不规定最长，不能保证答案的正确性。后面的证明会提到。

现在我们的首要问题是，如何求 $nxt$ 数组？

我们假定 $i$ 之前的答案都已经求出，现在需要求 $nxt[i]$。

我们设 $j$ 为 $nxt[i-1]+1$，如下图：

最简单的情况自然就是 $B[i]=B[j]$，那么 $nxt[i]=j$，这是显然的。

但是也可能遇到更棘手的情况：

$B[i]\neq B[j]$，怎么办呢？

既然YABAPQYAB这个公共真前后缀不行，那就再找一个更小的！

显然更小的前后缀就是YAB了，怎么得来的呢？就是看 $nxt[j-1]$ 的值是多少，那么新的 $j$ 就是 $nxt[j-1]+1$。此时再看看 $B[i]=B[j]$ 是否成立。成立的话就 $nxt[i]=j$，不成立就继续找 $j$，直到找到 $B[i]=B[j]$，或者 $j=1$ 为止。

可以发现我们充分利用了之前计算出的$nxt$，将原规模逐步缩小，是不是有点归纳法的意味？

再来举一个不断更新 $j$ 直到 $j=1$ 为止的例子：

我们可以把这一步骤也写成代码（下标从 $1$ 开始）：

int i=2,j=1;//nxt[1]应为0，所以i从2开始

while(i<=m){

	if(b[i]==b[j]) nxt[i++]=j++;

	else if(j>1) j=nxt[j-1]+1;

	else nxt[i++]=0;

}

（是不是和上面的代码很像）

至此把两个代码拼接起来就能得到 KMP 的全过程了。

P3375 【模板】KMP

下标从 $1$ 开始

#include<bits/stdc++.h>

#define N 1000010

using namespace std;

string a,b;

int n,m,nxt[N];

int main(){

	cin>>a>>b;

	n=a.size(),m=b.size();

	a=' '+a,b=' '+b;

	int i=2,j=1;

	while(i<=m){

		if(b[i]==b[j]) nxt[i++]=j++;

		else if(j>1) j=nxt[j-1]+1;

		else nxt[i++]=0;

	}

	i=1,j=1;

	while(i<=n){

		if(a[i]==b[j]) i++,j++;

		else if(j>1) j=nxt[j-1]+1;

		else i++;

		if(j==m+1) cout<<i-j+1<<"\n";

	}

	for(int i=1;i<=m;i++) cout<<nxt[i]<<" ";

	return 0;

}

下标从 $0$ 开始

#include<bits/stdc++.h>

#define N 1000010

using namespace std;

string a,b;

int n,m,nxt[N];

int main(){

	cin>>a>>b;

	n=a.size(),m=b.size();

	int i=1,j=0;

	while(i<m){

		if(b[j]==b[i]) nxt[i++]=++j;

		else if(j) j=nxt[j-1];

		else nxt[i++]=0;

	}

	i=0,j=0;

	while(i<n){

		if(a[i]==b[j]) i++,j++;

		else if(j) j=nxt[j-1];

		else i++;

		if(j==m) cout<<i-j+1<<"\n";

	}

	for(int i=0;i<m;i++) cout<<nxt[i]<<" ";

	return 0;

}

正确性证明

我们刚接触 $nxt$ 的定义时，可能会有疑问：为什么 $nxt$ 一定要表示 $B[1\sim x]$ 这一段的最长公共真前后缀长度？

我们证明一下 KMP 的正确性，顺带解决这个问题。

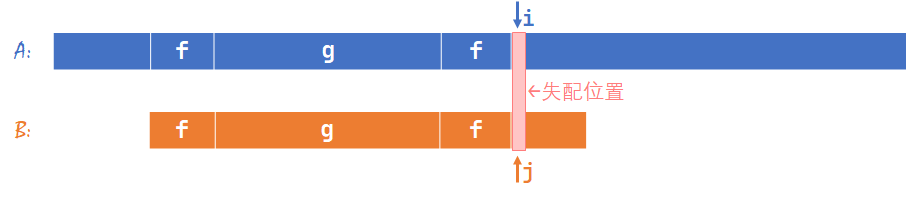
根据 KMP 的流程，如果遇到失配的情况，我们先找 $B[1\sim (j-1)]$ 中的最长公共真前后缀（如图，用 $f$ 表示）的长度 $nxt[j-1]$，然后把 $j$ 置为 $nxt[j-1]+1$，如下图。

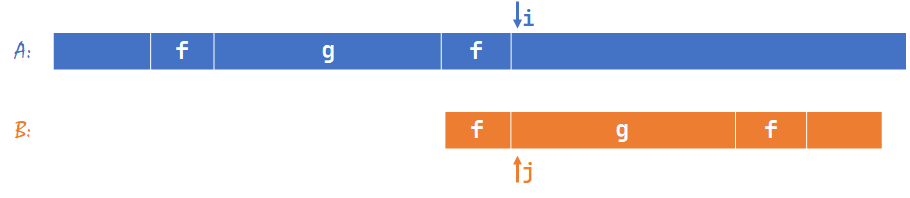
要证明 KMP 是正确的，首先需要证明 $j$ 回退时不会跳过正确答案。

我们假设在 $j>nxt[j-1]+1$ 时存在匹配，如下图，那么灰色箭头连接的部分都相等。

自然，黄色大括号部分（不包含 $i,j$）也相等，那么黄色部分的长度 $=j-1$。

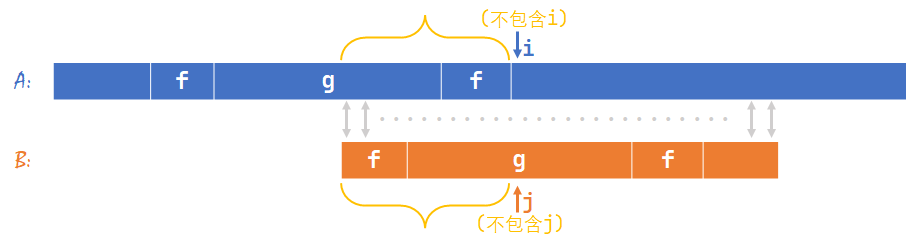
回到第 $1$ 张图（$j'$ 表示第 $1$ 张图情况下的 $j$），根据假设，$j>|f|+1$，即黄色部分长度 $>|f|$。

这样的话，黄色部分就成了 $B[1\sim j']$ 最长的公共真前后缀，与“$f$ 是 $B[1\sim j']$ 最长公共真前后缀”矛盾。

得到的结论是：$j>nxt[j-1]+1$ 时一定不存在匹配。

这样我们的问题就迎刃而解了：如果 $nxt$ 不是最长，上面的情况就可能不形成矛盾，进而 $j>nxt[j-1]+1$ 时也可能存在解，而这被我们忽略掉了，所以正确性不能保证。

但正确性证明还没完，我们还需要考虑 $j<nxt[j-1]+1$ 的情况。

事实上，这种情况是可能存在答案的，但我们可以证明，如果每次失配 $j$ 都回退到 $nxt[j-1]+1$，一定可以把这种情况的答案找出来。

还是图 $1$ 的初始状态，现在 $A[i]\neq B[j]$，发生失配。我们现在让 $j<nxt[j-1]+1$：

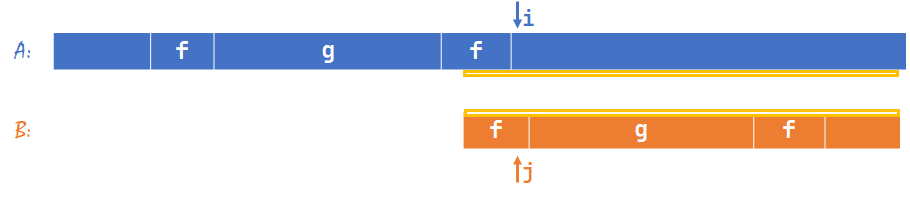
也就是 $j$ 现在在 $f$ 里面了。现在我们的问题是：如果这种情况下存在答案，我们按 $j=nxt[j-1]+1$ 的步骤，是否能找出这个答案？

我们假设在 $j<nxt[j-1]+1$ 中存在答案，如上图黄色线段所示。

现在我们让 $j=nxt[j-1]+1$：

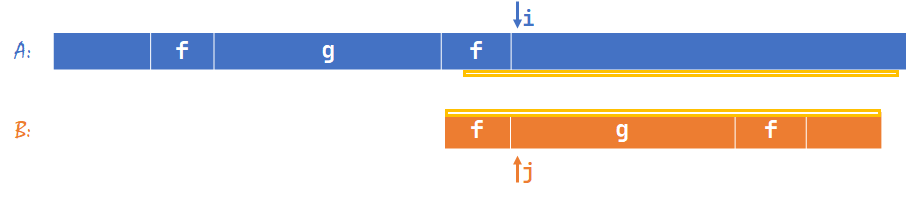
我们继续匹配，那么这一轮的失配位置一定 $j\in [nxt[j−1]+1,m+1]$（$j=m+1$ 就是匹配成功）。

如下图，虚线位置即失配位置。

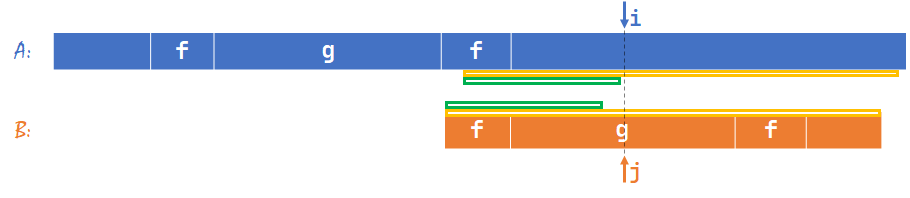
如上图，如果绿色线段就是 $B[1\sim (j-1)]$ 的最长公共真前后缀，那么下一轮应该将两个绿色线段对齐继续匹配，这样黄色线段这个答案就被找到了。

如果不是呢？

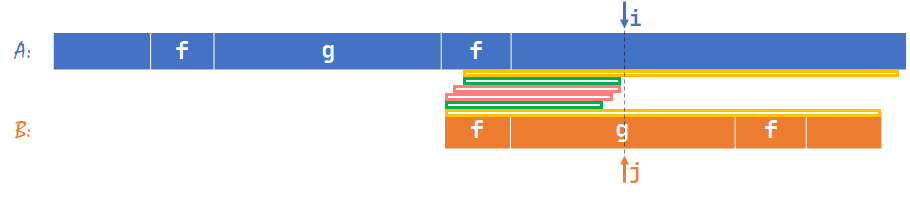
如上图，假设粉色部分是真正的公共前后缀，那么我们接下来应该把 $j$ 回退到粉色的下一个位置：

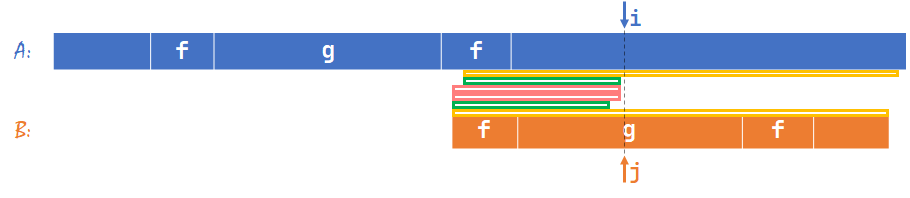
此时两个粉色重合。我们可以发现，这和上上张图的情形类似，只不过两个绿色离得更近了。这样重复上面的过程，再找第 $1$ 个失配位置，不断逼近，总有一次绿色部分会成为 $B[1\sim (j-1)]$ 的最长公共真前后缀。至此，我们证明了如果 $j<nxt[j-1]+1$ 存在答案，按我们的方法一定能找到它。

综上，KMP 的正确性得证。

复杂度证明

通过看代码能发现两部分实现相似，所以就一块说了：

$i$ 每增加 $1$，$j$ 最多也增加 $1$，从而 $j$ 最多增加 $len$ 次，进而最多减少 $len$ 次。

所以处理 $nxt$ 是 $O(m)$ 的，主过程是 $O(n)$ 的，总时间复杂度就是 $O(n+m)$ 了。

——字符串学习笔记 · 浅析KMP——单模式串匹配算法 - 皎月半洒花

细节

术语

我们前面提到的 $nxt$ 数组，其实叫做PM表（Partial Match Table，部分匹配表）。

真正意义上的 $next$ 数组，就是把PM表整体右移一位，最后一个值舍弃掉，然后在第 $1$ 位补 $-1$。这个似乎并不常用，因为最后一个值舍弃掉了，所以只能匹配一次。

代码实现

KMP的代码，网上有很多种写法，有和上面放的代码一样的while类型写法。

当然你也可以变一下，用for循环套while，效果是一样的。具体用哪个看你的选择。

下标从 $1$ 开始

#include<bits/stdc++.h>

#define N 1000010

using namespace std;

string a,b;

int n,m,nxt[N];

int main(){

	cin>>a>>b;

	n=a.size(),m=b.size();

	a=' '+a,b=' '+b;

	for(int i=2,j=1;i<=m;i++){

		while(b[i]!=b[j]&&j>1) j=nxt[j-1]+1;

		if(b[i]==b[j]) nxt[i]=j++;

	}

	for(int i=1,j=1;i<=n;i++){

		while(a[i]!=b[j]&&j>1) j=nxt[j-1]+1;

		if(a[i]==b[j]){

			if(j==m) cout<<i-j+1<<"\n";

			j++;

		}

	}

	for(int i=1;i<=m;i++) cout<<nxt[i]<<" ";

	return 0;

}

下标从 $0$ 开始

#include<bits/stdc++.h>

#define N 1000010

using namespace std;

string a,b;

int n,m,nxt[N];

int main(){

	cin>>a>>b;

	n=a.size(),m=b.size();

	for(int i=1,j=0;i<m;i++){

		while(b[i]!=b[j]&&j) j=nxt[j-1];

		if(b[i]==b[j]) nxt[i]=++j;

	}

	for(int i=0,j=0;i<n;i++){

		while(a[i]!=b[j]&&j) j=nxt[j-1];

		if(a[i]==b[j]){

			if(j==m-1) cout<<i-j+1<<"\n";

			j++;

		}

	}

	for(int i=0;i<m;i++) cout<<nxt[i]<<" ";

	return 0;

}

还有很多写法是把上面代码的 $j$ 整体 $-1$ 来使用，本质上是一样的，不过代码实现需要先j++才能得到与$i$匹配的位置。就不放代码了。

不同写法原理都是一样的，不要拘泥于细节，根据自己的习惯使用即可。

$\mathcal{NEXT\ \ \ PHANTASM...}$