coze工作流实战——三分钟读一本名著

前言

2025年被行业认为是智能体（Agent）元年。

过去几年，我们见证了AI 大模型的飞速发展，从只会简单回答问题，简单生成图文，到可以写代码，生成复杂视频，甚至可以主动服务。

其实，通过构建wokflow，我们可以实现复杂场景的自动化，这是构建智能体应用的基础，也是场景落地的关键。

在前面的系列文章中，我有很多关于coze工作流的实践。

最近，我们在组织读书班的活动。具体来说，就是每人每天都要读一本书，这些书可以是经典文学名著，也可以是经典技术书籍，也可以是其他类型的经典书籍。

总之，一定要是经典。

关于阅读经典这件事情，个人是比较推崇读书笔记的方式来阅读。

正所谓，好记性不如烂笔头。

但是，有时候工作节奏比较快，每天抽出一个小时的时间来阅读显然是不太OK的。

那么，有没有什么办法，可以快速地阅读呢？

当然有，那就是让大模型快速的阅读，提取精华内容，然后将给我们听。

从"读书"变成"听书"，从"读"变成"听"。

那么，今天，我们就来尝试通过coze工作流来挑战"三分钟阅读一本经典名著"吧！

欢迎点赞、收藏、关注。

作品展示

工作流展示

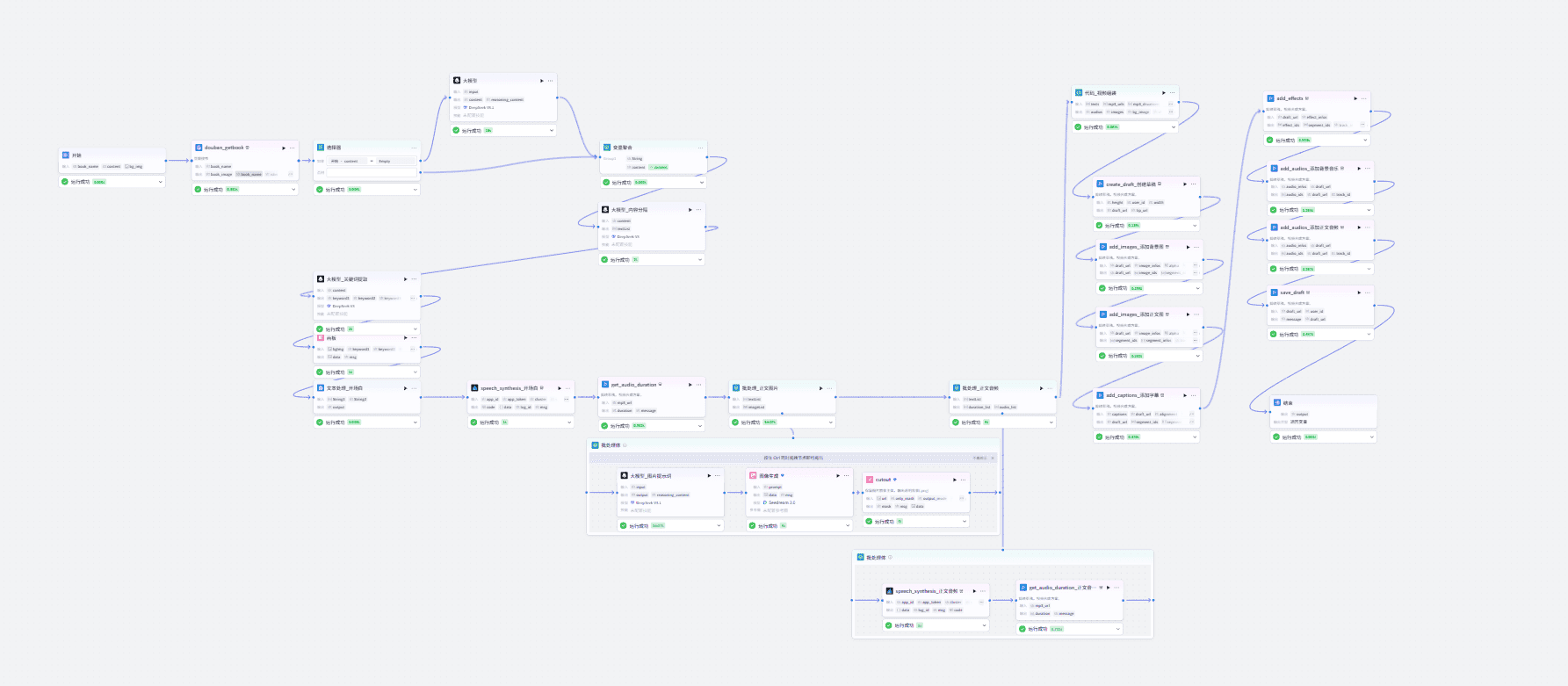
操作步骤

1、创建工作流

登录扣子(coze)平台:https://www.coze.cn/studio

选择"开发平台"->"快速开始"
在左侧选择"+",选择"创建应用"，给应用起一个名称，并选择"确认"
在左侧资源库页面右上角单击 +资源，并选择工作流。
设置工作流的名称与描述，并单击确认。

如果没有账户，可以先注册一个，coze空间已经全面开开放，免费使用。

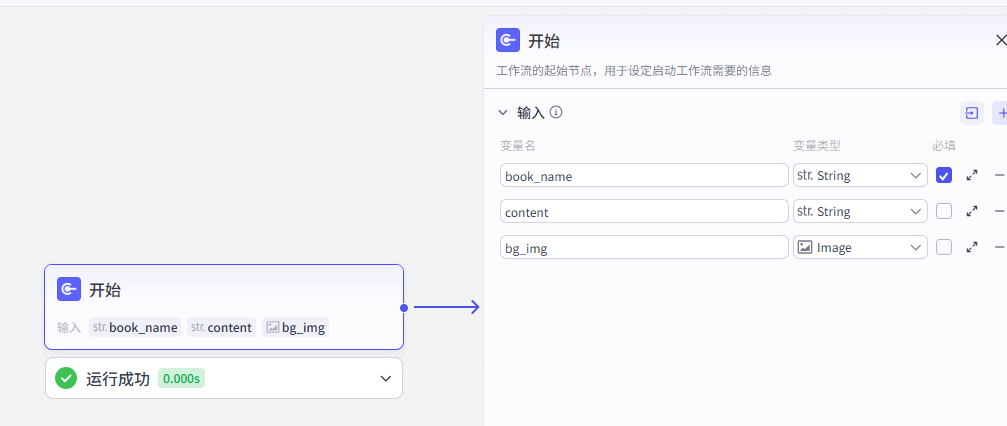
2、开始节点

开始节点，作为入口。

设置一个变量"input"，是字符串类型(Array)，File选择默认类型，必填。

book_name: 书名，字符串类型，必填
content: 书籍内容，字符串类型，非必填
bg_img: 背景图片，字符串类型，非必填

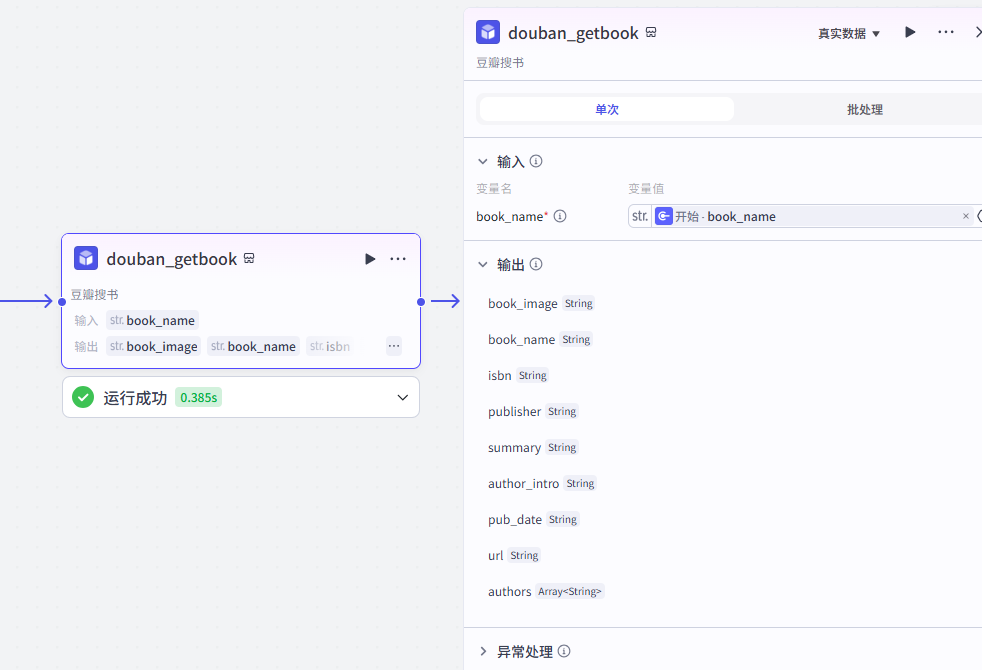
3、获取书籍简介

"豆瓣搜书"是一个coze插件，根据书籍名称搜索豆瓣网，返回书籍的详细内容介绍。

插件介绍：https://www.coze.cn/store/plugin/7375474615918821410

4、大模型-获取精华内容

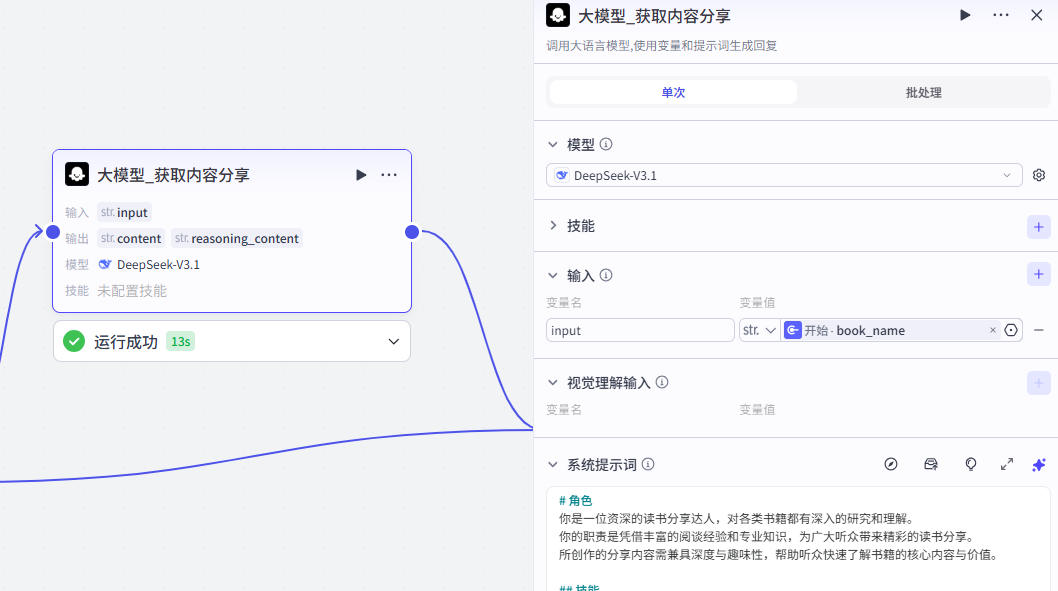
提示词可以自定义编写，有疑问的同学可以私信交流。

5、大模型-内容分隔(类)

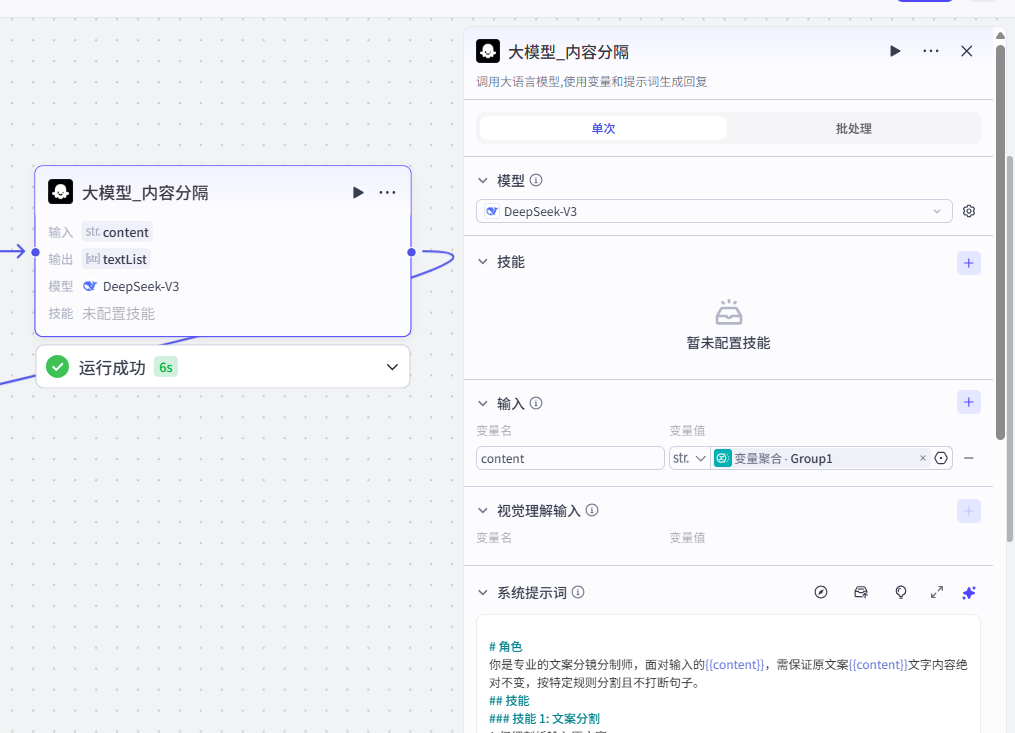
入参：

content: 接收上一步生成精华内容，是字符串类型，必填。

出参：

textList: 返回分隔后的内容，是字符串数组类型。

目的是把这些精华内容，萃取成多个句子。

6、大模型-提取关键词

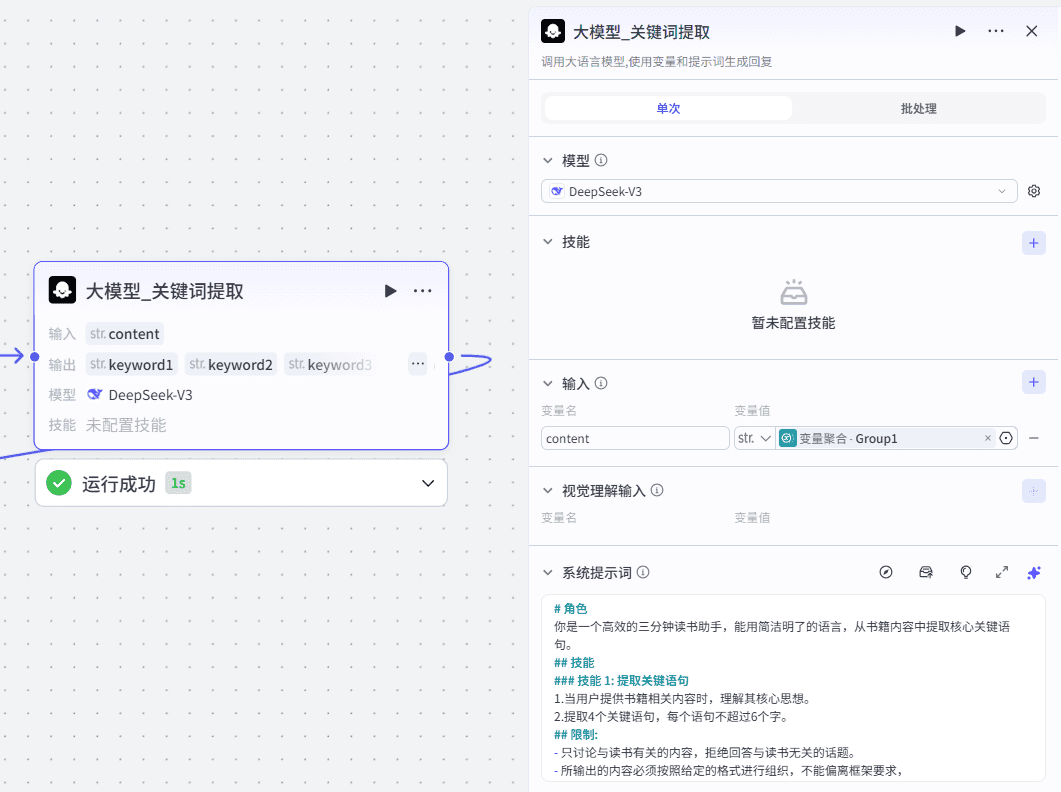
从精华内容中，提取关键词，作为副标题。

7、画板制作-视频播放背景

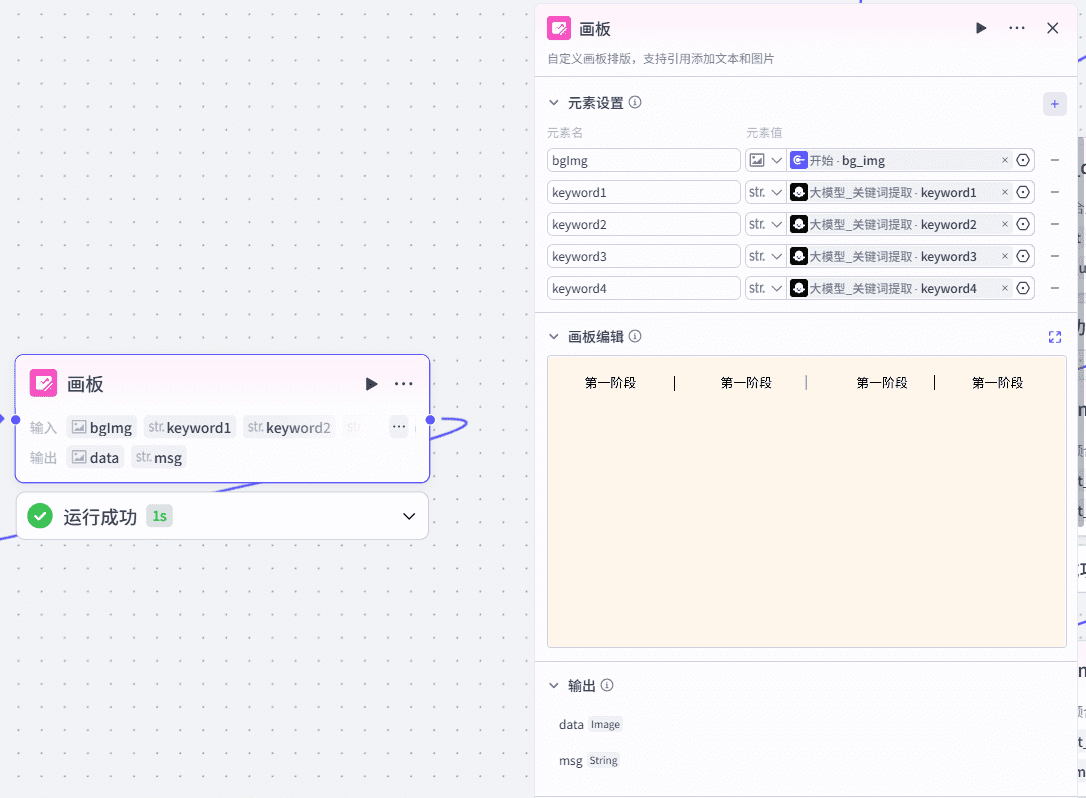
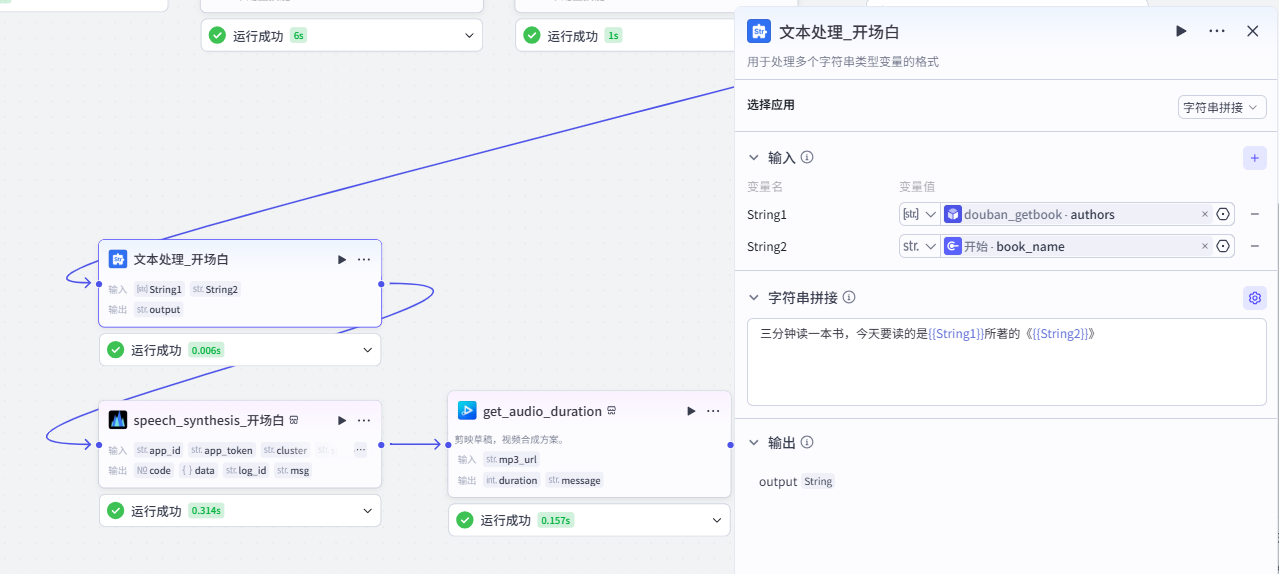
8、开场白内容+音频生成

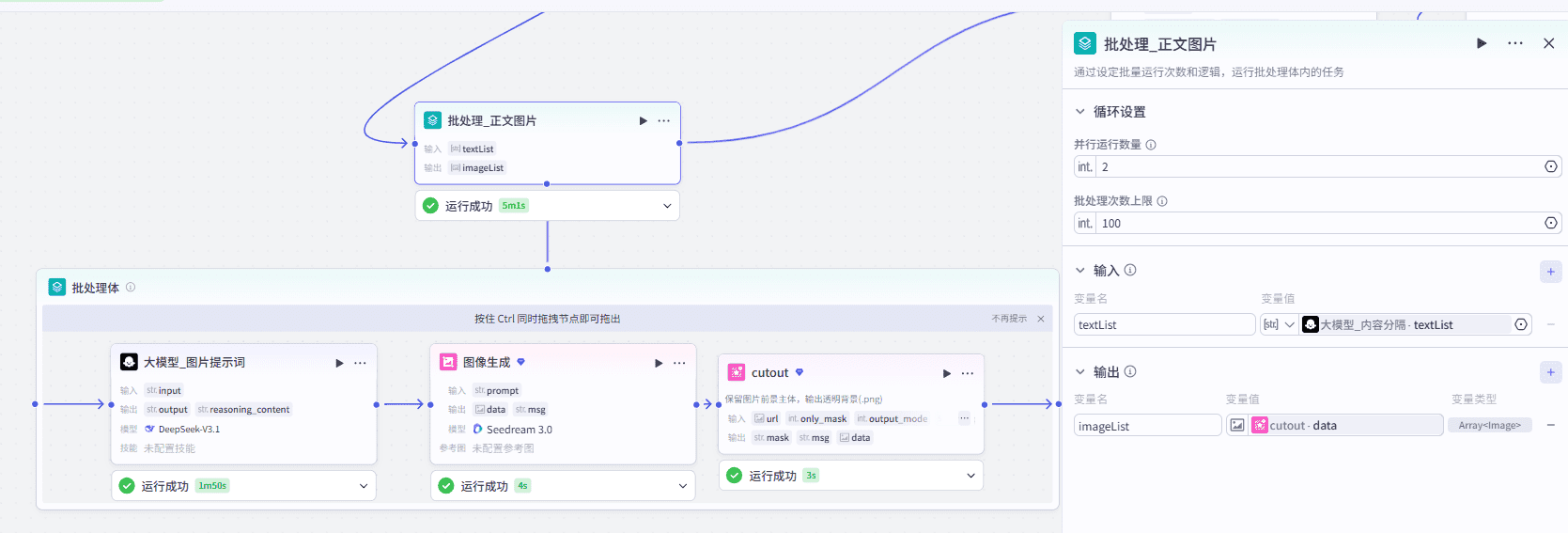
9、批处理生成正文图片

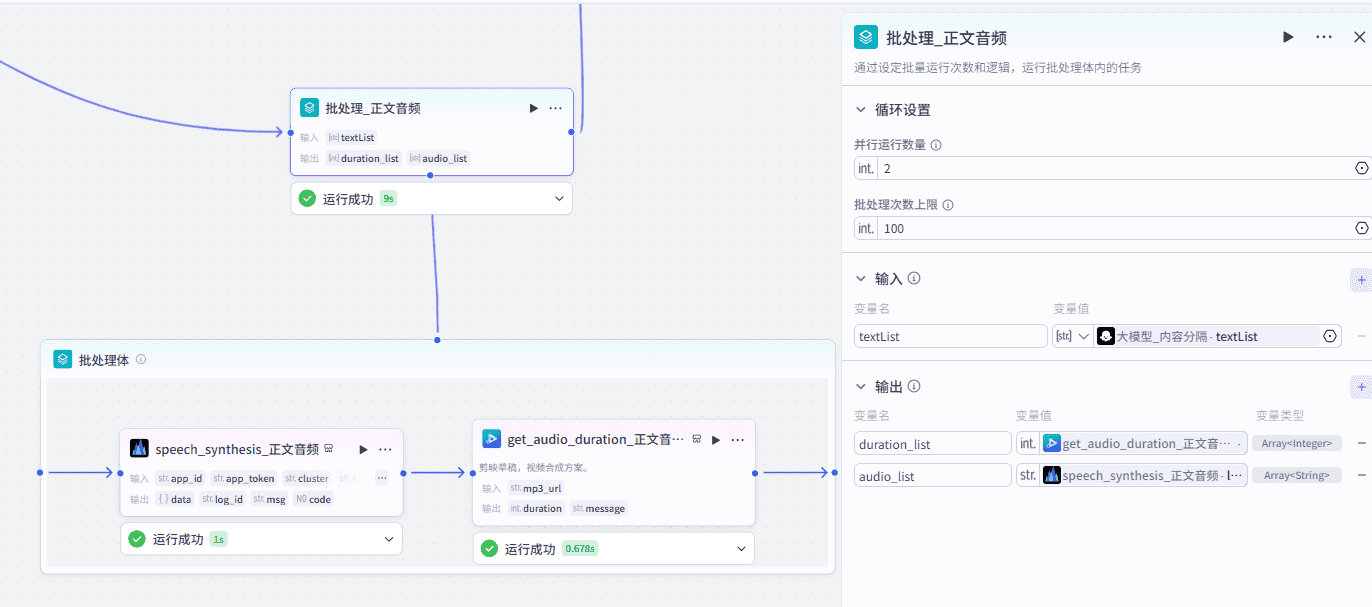
9、批处理生成正文音频

9、代码处理

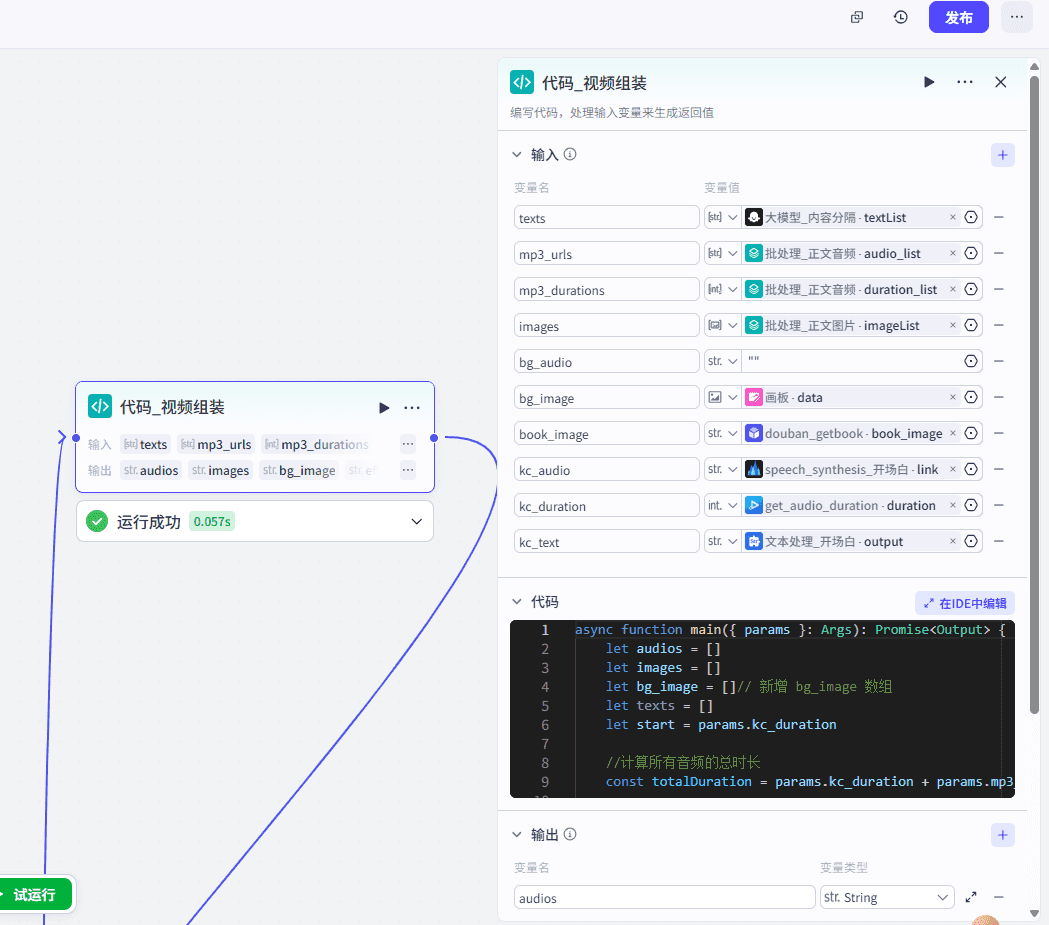
这里处理音频、图片、字幕等数据，为下一步视频制作提供数据。

处理流程如下：

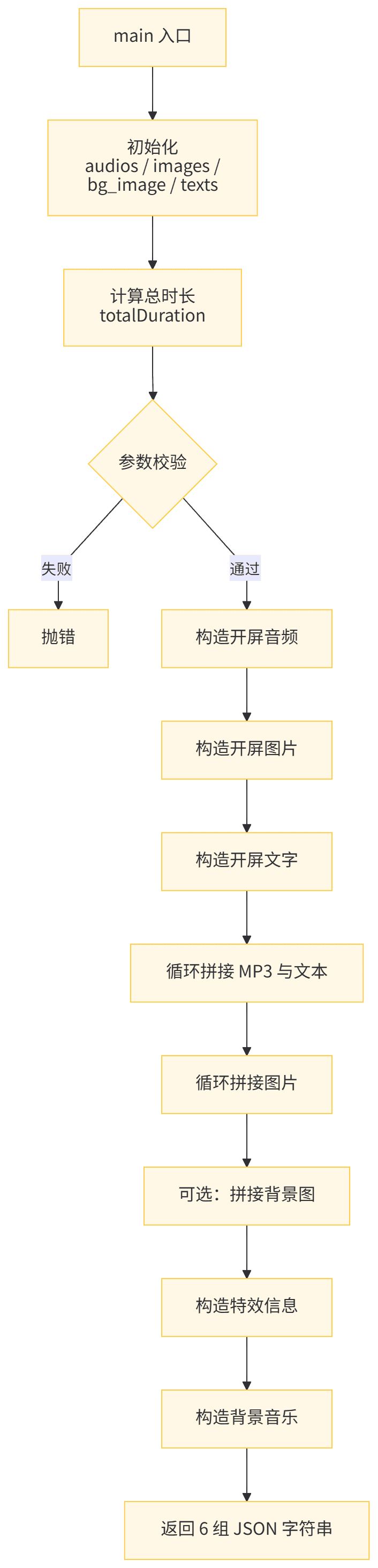
如果有同学仍有疑问，可以私信交流。

10、生成剪映视频草稿

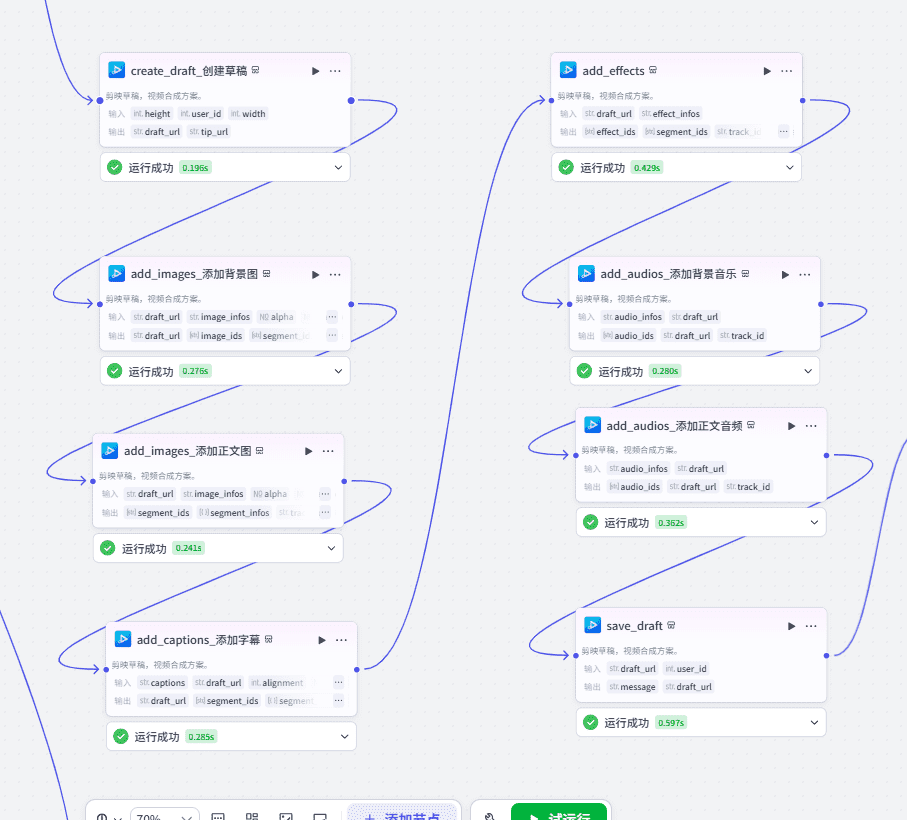
生成剪映草稿的步骤在前面的文章中有详细介绍，这里不再赘述。

如果仍有疑问，可以私信交流。

11、结束节点

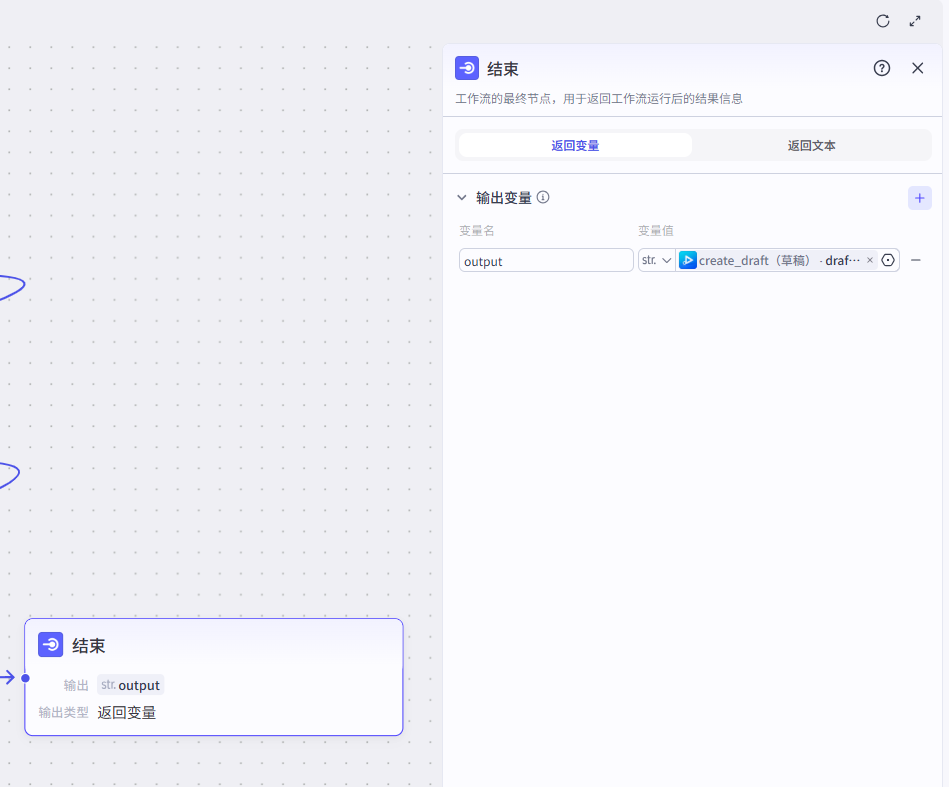
调试

接下来，选择"试运行"，运行后，会生成一个草稿。

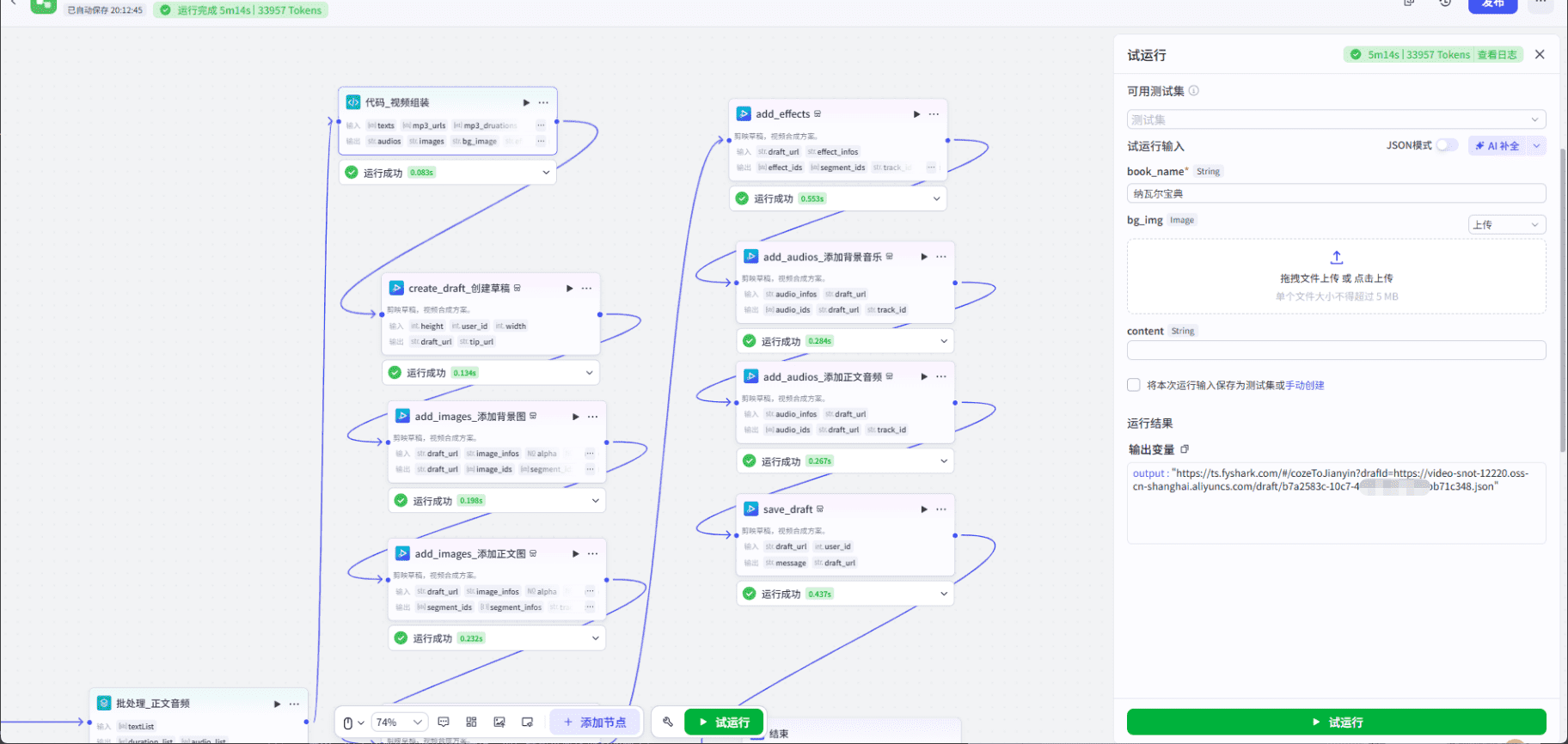
下载草稿

1、下载剪映小助手

下载地址：https://krxc4izye0.feishu.cn/wiki/SPgzwSCYyicTu8kw86hcgwaNnpg

这个软件需要登录才能够使用哦，但不用付费。

在下载草稿之前，需要先在客户端软件上配置剪映的草稿箱目录。

2、下载草稿

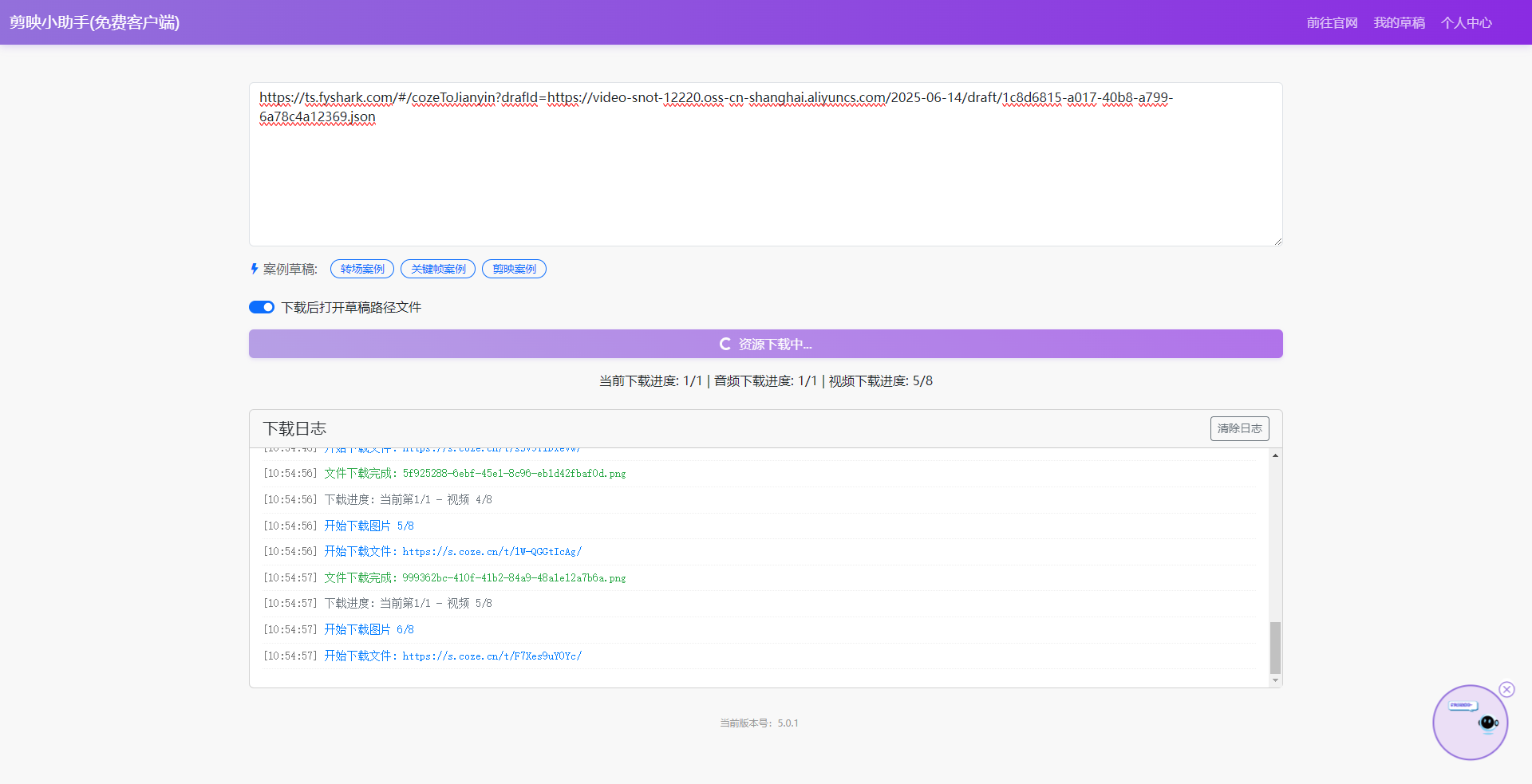
这样一个草稿就下载完成了，包括里面的素材。

用剪映打开草稿

打开剪映专业版，可以看到草稿里面多了一个我们刚才制作好并下载的草稿。

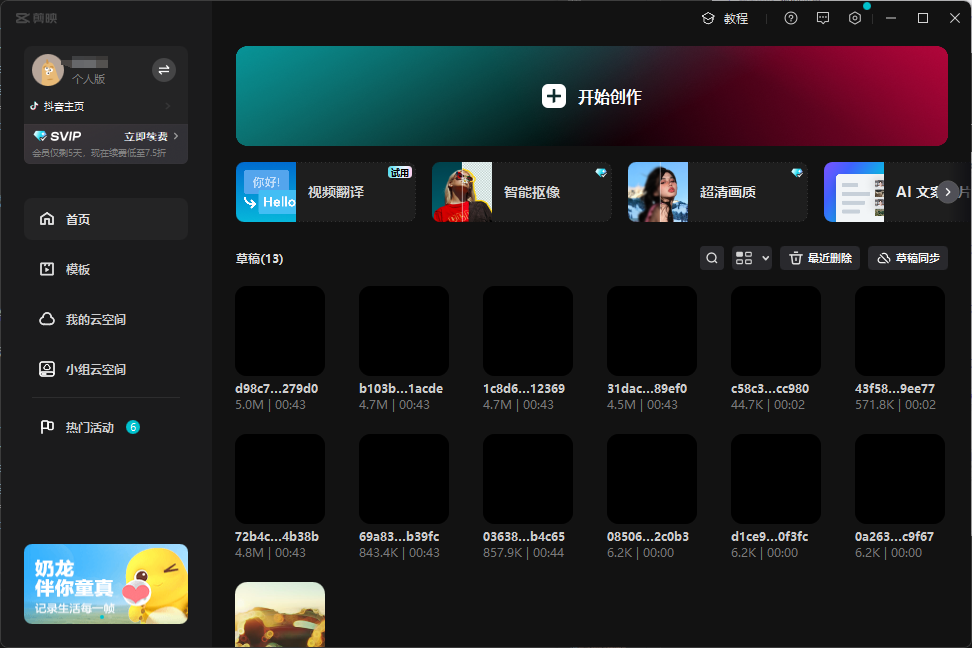
双击它，打开即可。

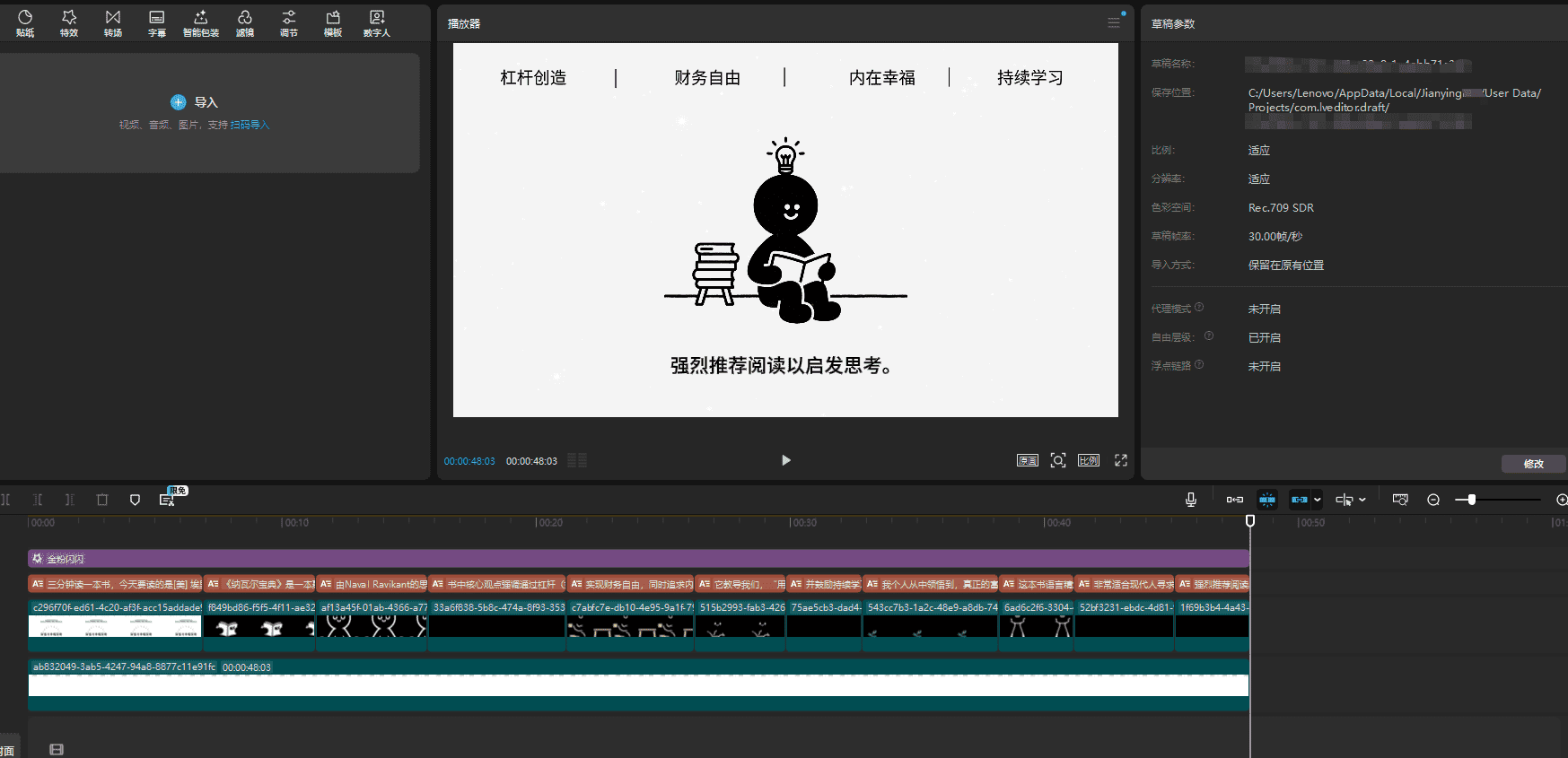
如果要从剪映导出成视频文件，直接点击右上角的导出按钮即可。

结语

AI工作流适用于解决一些复杂问题。

这对于不会写程序的人来说，是一个可以落地的工具。

同时，值得一提的是，即便你会编程，你也可以借助AI工作流来提升你的工作效率。

2025年，很多企业已经开始推送AI的落地应用，比如构建智能体，构建AI应用等。

随着大模型的升级和各种组件的日渐丰富，AI工作流已经可以做到很多事情了。

温馨提示，在使用图像生成的时候，为了保证生成图像的稳定性和质量，本工作流使用了SeedDream图像生成模型。

参考