python：冒泡排序（Bubble Sort）超详细教程！

关于排序，真的非常的重要。数据可以从小到大排序，也可以从大到小排序。这样对于一个有序的数据，我们处理起来就很方便，这对于我们的工作帮助是很大的。

那么你拿到一组无序的数据，你将要如何去处理它呢？

冒泡排序就是从一个可迭代容器里，用某一索引去和它的下一个索引做比较，如果大于它的下一个索引，它们就交换位置。反正就是通过交换，使得大的数据在小的数据后面，使得数据的顺序满足从小到大的顺序。

我查阅资料的解释是这样的：

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

直观一点的解释就是：

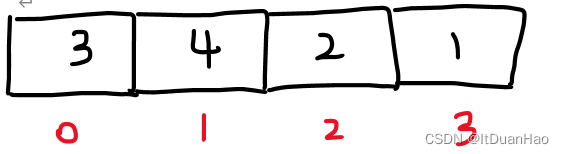
如果我们想要得到一个正序的列表。开始的时候，0索引的数据和1索引的数据比较，显然3小于4，那么就不交换。然后比较1索引的数据和2索引的数据。4大于2，所以交换：

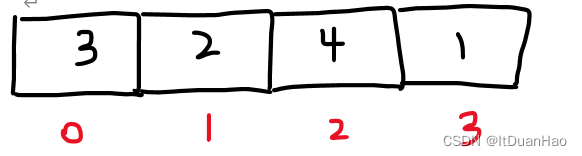
之后，2索引的数据和3索引的数据比较，4大于1则交换。那么4就到了正确的位置上，我们重复以上的操作，0索引的数据和1索引的数据比较……经过这个操作3就到了正确的位置上。我们发现每次从0索引比较过去，就会有一个数据落在正确的位置上。

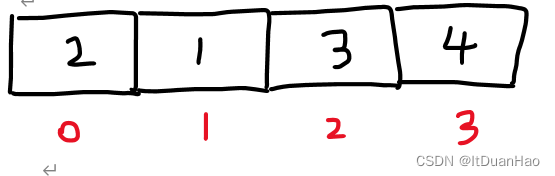
我的容器里面有4个数据，那我们是不是循环四次，从索引比较过去就能把所有的数据落在正确的位置。其实只需要三次循环就行，4个数据里，其他3个数据都落在正确的位置，那么最后一个数据一定也是在正确的位置上，是不需要额外加一次循环排序的。

我们再理一下思路：

如果有n个数据，我们循环n-1次，每次循环都从0索引到2索引交换排序。

我们进行的编程的时候也要进行循环的嵌套。

具体的代码：

for i in range(len(li)-1):  #  n个数据循环n-1次
        for j in range(len(li)-1-i): # 0索引到2索引
            if li[j] > li[j + 1]:  # 比较数的大小后交换
                li[j], li[j + 1] = li[j + 1], li[j]

被嵌套的那个循环里面是len(li)-1-i，这个意思是：后面已经落到正确位置的数据是不需要再进行判断然后排序的。i是外部循环的元素，i是几就代表有几个数据已经落到了正确的位置。这样应该就能很好的理解len(li)-1-i了吧。

如果代码像上面那样写并不是完美的，例如这样一组数据：

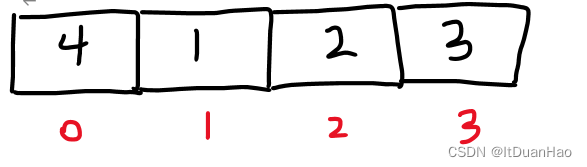
除了第一个数据，后面的数据已经是排好的。我们进行一次从0索引到2索引的交换就可以完成数据的排序。但是如果按上面代码的写法，就必须要循环三次，也就是后面的两次循环虽然进行了，但是并没有实际作用，是多余的。那么如何优化代码呢？

其实很简单，每进行一次外循环，我们把一个exchange变量赋予False值。每一次内循环比较条件成立，就把exchange变量改成True。然后我们加一行判断条件，如果not exchange为True就return结束循环。

def buble_sort(li):
    for i in range(len(li)-1):  # n个数循环n-1次
        exchange = False
        for j in range(len(li)-1-i):
            if li[j] > li[j + 1]:  # 比较数的大小后交换
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True
        if not exchange:
            return

如果没弄明白，多看几遍，自己理一下思路就差不多了。