JOI 简单题选做

就是把洛谷上评分为紫的题做了一下（汗）

前两道题没做出来，暴露了自己在 dp 上的短板。

イベント巡り 2

一开始想到贪心，但发现我们只要选 \(k\) 个即可，所以可以尝试一些更劣但是编号更小的做法。

但贪心做法还是有借鉴价值的，对于一个时间区间，我们还是可以用贪心求出能放多少个活动。更进一步，这个过程可以倍增优化。

我们已经知道了一个区间最多能放多少个区间了，于是我们可以贪心看编号最小的点能不能放，如果能就放。但放完以后我们的区间会发生变化，所以我们实际上统计的是初始区间能放的最大的活动-当前区间能放最大的最大活动能不能 \(<= k\)。

如果能，要裂开原始区间，原因显然。

集合写真

最终序列就是这样子~

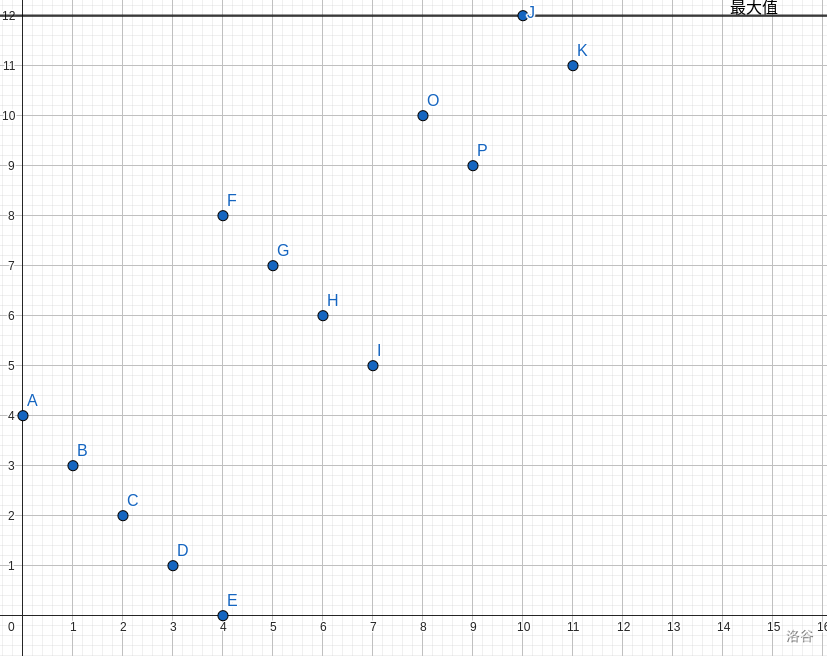
由若干个严格单调递减（且相邻元素差为 \(1\)）的数列组成的序列~

定义 \(dp_i\) 为让前 \(i\) 个元素变成合法，且最后一个单调递减序列的终点在 \(i\) 时的最小代价~

于是 \(dp_i = max(dp_j + calc(j + 1, i))\)。根据 \(dp\) 的定义，不难发现最终 \(j+1\) 到 \(i\) 组成的序列是固定的~

我们来算贡献，对于 \(calc(l, r)\)， 我们暴力统计，考虑数对 \((i, j)\) （保证 \(i\) 小于 \(j\)）:

如果 \(a_i,a_j<=l\)，贡献在 \(dp_{i-1}\) 里算过了，忽略。

如果 \(a_i>=r\)，只有当 \(l<=a_j<=r\) 时才产生 \(1\) 的贡献。

如果 \(a_i,a_j\) 都在 \(l\) 到 \(r\) 内，顺序时产生贡献。

然后开两个树状数组优化求后两个部分就行。

フードコート

离开事件是没有必要的，只要把白嫖事件的人数加上离开事件的人数即可。

思考一下如何求离开人数。我们使用线段树统计当前人数，树状数组统计剔除离开事件的人数，当线段树执行减操作时，我们需要额外的一个懒标记表示当前结果要与 \(0\) 取 max。

void change(int u, point p){
    tr[u].val += p.addTag;
    if(tr[u].maxTag > -inf) tr[u].maxTag += p.addTag;//如果没有懒标记就不用加了，否则万一加到正数了呢
    tr[u].addTag += p.addTag;
    //----------------------进入max环节~
    tr[u].val = max(tr[u].val, p.maxTag);
    tr[u].maxTag = max(tr[u].maxTag, p.maxTag);
}

然后我们整体二分，如果加入当前家庭后大于询问的 \(B\)，当前家庭就是答案。这部分比较简单，不再赘述。

ビーバーの会合 2

先考虑链~

一个点时怎么办?就是 1 呗，还想咋样-_-||

两个点时怎么办？放在链的两端，可以达到 \(n\) 的大小！

三个点时怎么办？考虑当前点 \(u\) 为距离和最小的点，然后发现无论往哪边移，要么是两加一减，要么是两减一加（这是不可能的，因为当前点已经最小了），所以只可能有一个点。

四个点时怎么办？放在第二个和倒数第二个，就是 \(n-2\) 的大小！

第五个时怎么办？看看三个点时的情况吧！

对于所有奇数，答案都是 \(1\)！

我们发现，最终的路径一定是一条路径的长度，我们选择的点平均分布在路径端点的两边。这时我们把汇合点在路径上移动，增加的距离和减少的距离会相抵。

放到树上，就是平均分布在路径端点的子树中了。

于是可以点分治！我们只需要求出当前路径可以达到的总数最大值，那么就可以最后一起最大值更新到最小值了！

Commuter Pass

首先看到第二个部分分：从 \(S\) 到 \(T\) 只有一条最短路径。这意味着 JOI 君的通勤票是固定的。因此我们把路径分成三个部分：

1. 从 \(U\) 到这条最短路上任意一个点
2. 在最短路上穿行
3. 跳出最短路走到 \(V\)。

不难发现第二个部分代价为 \(0\) 。因此我们只需要找到从 \(U\) 走到最短路的最短距离与最短路走到 \(V\) 的最短距离。把第三个部分倒过来就可以用两次最短路求解。

注意样例二告诉我们了一种情况，就是 \(S\) 到 \(T\) 的最短路与我们最终走的路径没有一条重叠的边。所以最终答案要与直接从 \(U\) 走到 \(V\) 的最短路做比较。

现在我们看到满分做法，有了多条最短路。一个显然的思路就是在 dijkstra 松弛时顺便记录这条路径哪一个点与 \(U\) 距离最短，哪一个点与 \(V\) 距离最短。如果你对松弛时进行操作是否能统计完全所有情况抱有疑问，请参考 P1144 最短路计数。

多条路径的交点怎么处理？显然，如果一条路径上到两点的最小距离之和优于另一条路径，那么我们要一并更新当前点到两个点的距离，不能出现分开的情况（即到 \(U\) 距离最小的点，到 \(V\) 距离最小的点不在同一条路径上）。

当然，将新的路径与原路径进行比较时，要先用当前点到 \(U\) 和 \(V\) 的距离更新新路径上的最小距离。

注意当最短距离发生变化后，我们要重置当前点所在路径存储的信息后再开始比较。因为之前的信息都不是最短路径的。

首都

如果颜色 \(u\) 需要与颜色 \(v\) 合并后才能到达，我们就将 \(u\) 和 \(v\) 连有向边。到了最后这就变成了一个有向图，其中的环都是需要互相合并的，于是我们缩点。

在缩完点后的 DAG 上，我们寻找出度为 \(0\) 的，含原来的点最少的点，就是我们的答案。因为这个点（环？）所需的合并次数最少。

怎么连边呢？显然，边数可能很大！最大可以建满！于是我们树剖后用线段树优化建图即可。

注意一件事：我们要把线段树的叶子节点（代表原树上的一个节点）连向他的颜色，因为最终我们是在颜色间连边。

独特都市

点 \(u\) 的独特城市分两种：在 \(u\) 深度最深的子树里的，和深度虽然不深但当前深度只有一个的。显然，这两者都是在 \(u\) 到直径的一个节点的路径上的。

我们求出直径，从两个端点各算一遍每个点到这个点路径上的独特城市，对于每个点去最大值即可。

怎么求？我们开个栈，存储当前的独特城市。具体如下：

1. 将父亲入栈
2. 将与当前点距离小于等于次长链长度的点都删去。这些点无论在这个点的哪棵子树中都不可能成为独特城市。
3. 遍历最长链所在子树
4. 用当前栈求出当前节点的答案
5. 将与当前点距离小于等于最长链长度的点都删去。这些点只会对最长链所在子树产生影响。
6. 遍历其他子树

星座3

贪心，从最下面一行开始，比较删除这颗星与删除与这颗星成矩形的所有点哪个代价更小。留下代价更小的那一方

道路の建設案

切比雪夫距离就涉及到我的知识盲区了-_-||

我们套路地二分第 \(k\) 小的距离，判断比他小的有多少个。

把曼哈顿距离转为切比雪夫距离后，判断大小就变成了二维数点问题了。这道题用 set 一个一个跳，每次二分最多跳 \(k\) 次，所以复杂度为 \(O(n \log k)\)。

后记

写一篇博客，发现有几道题自己的做法都不太记得了。。。所以复习还是很重要的！