运筹学之线性规划 1.X

线性规划

线性规划问题的标准形式可以写成：

\[\begin{aligned}
&max~z=\pmb{c}^T\pmb{X} \\
&s.t.\{
\begin{aligned}
&\pmb{A}\pmb{X}=\pmb{b}\\
&\pmb{X}\geqslant0
\end{aligned}
\end{aligned}
\]

，\(\pmb{X}\)是列向量

---

为什么可以统一为这个标准形式 ？

1. 所有约束都可以写成等式约束是因为在初始决策变量不足的情况下，我们可以加入非负的松弛变量到不等式中，使其变成等式约束。

2. 之所以可以将决策变量约束为非负是因为，决策变量的符号有三种可能

• 首先是非负的，这种情况下我们无需改变
• 第二种情况是决策变量是非正的，那么我们只需用相反的变量取代即可
• 第三种情况是决策变量没有符号要求，那么我们就可以定义两个非负变量进行相减来替代这个没有符号要求的决策变量。

线性规划的解有四种可能：

• 唯一解
• 无穷多解
• 无界解（即目标函数可以在约束条件下达到无穷进而使得无解）
• 无可行解（即不存在满足约束条件的解）

单纯形法

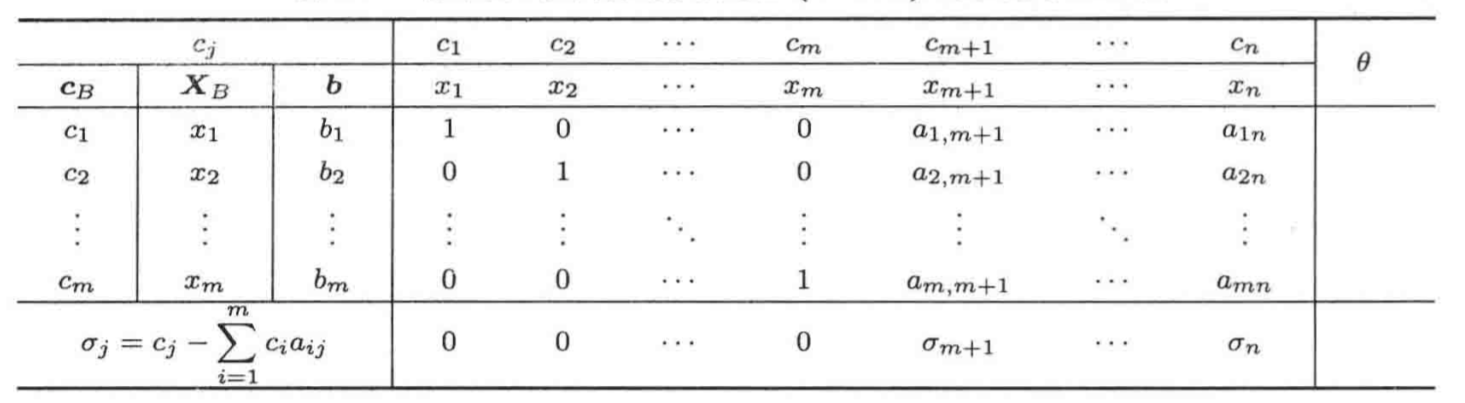
单纯形表

计算步骤(求极大)

(1) 确定一个初始基可行解

(2) 计算非基变量的检验数

判别准则:

1. 若所有非基变量检验数都小于或等于零, 则原问题得到最优解
2. 当非基变量的检验数至少有一个为零, 原问题有无穷多组最优解, 但其目标函数值相等
3. 非基变量的检验数至少有一个大于零, 且某个大于零的检验数所对应的非基变量的系数列向量中没有正数, 则原问题具有无界解

(3) 基变换. 寻找检验数最大的列对应的变量, 将 \(b\) 分别除以这一列上的数得到 \(\theta\) 列, 再选定 \(\theta\) 最小的这一行对应的变量, 用最大的检验数对应的变量替换最小的 \(\theta\) 对应的 \(\boldsymbol{X}_b\) 处的变量

(4) 迭代

初始时, \(\boldsymbol{b}\) 需要大于零

右下角的函数值由 \(\boldsymbol{c}_B^\top\boldsymbol{b}\) 计算得

当算法停止时, \(\boldsymbol{X}_B\) 对应的 \(\boldsymbol{b}\) 取值即为解, 右下角的函数值即为最优函数值

停止算法条件

如果是求极大, 则当非基变量的检验数都小于等于0时停止

如果是求极小, 则当所有非基变量的检验数都大于等于0时停止

大M法

使用条件

当使用单纯形法时发现没有单位子矩阵

操作

通过加入人工变量拼凑单位子矩阵, 再运用单纯形法进行求解

• 当无解或者有解但最优解中至少还有一个人工变量时, 说明原问题无解.
• 当有解且最优解中不含有人工变量时, 其最优解就是原线性规划问题的最优解.

优点

可以直接求解问题

缺点

由于电脑无法输入任意大的数继续进行运算, 所以大M法只能手动运算

两阶段法

操作

• 第一阶段是构造一个目标函数只含有人工变量的辅助问题,再运用单纯形法进行求解.

• 当无解或者有解但目标函数不为零, 说明原问题无解, 终止
• 当有解且其目标函数值为零时, 则得到原问题的一个初始基可行解.

• 第二阶段是对第一阶段得到的单纯形表, 将其表头换位原问题的表头并且重新计算检验数