通过Precision/Recall判断分类结果偏差极大时算法的性能

当我们对某些问题进行分类时，真实结果的分布会有明显偏差。

例如对是否患癌症进行分类，testing set 中可能只有0.5%的人患了癌症。

此时如果直接数误分类数的话，那么一个每次都预测人没有癌症的算法也是性能优异的。

此时，我们需要引入一对新的判别标准：Precision/Recall来进行算法的性能评判，它们的定义如下：

可以看出，Precision表示：预测一件事件发生，它实际发生的概率是多少。换言之：预测准的概率如何。

Recall表示：一件事情实际发生了，能把它预测出来的概率是多少。换言之：预测漏的程度怎么样。

通过使用这两个标准，在测试集分布严重不均与的时候，就能有效的评判算法性能了。

在实际使用过程中要注意：要将出现概率极小但我们很关注的类的标签至为1，出现概率大的类标签置为0。

不过，设定两个标准又导致了一个trade-off的问题：我们在选择算法的时候，到底是更看重Precison还会Recall呢？

为了解决这种纠结，前人引入了一种叫F1 score或者F score的方式来进行评价算法。

它的计算公式为：

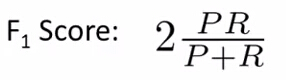
其中，P表示Precision值，R表示Recall值。

可以看出，当P、R中任何一个为0时，整个F1 score的值都是0，表示该算法很差。

当P、R都是1时，F1 score值是1，表示该算法非常好。