【BZOJ4766】文艺计算姬 [暴力]

文艺计算姬

Time Limit: 1 Sec  Memory Limit: 128 MB
[Submit][Status][Discuss]

Description

　　"奋战三星期，造台计算机"。
　　小W响应号召，花了三星期造了台文艺计算姬。
　　文艺计算姬比普通计算机有更多的艺术细胞。
　　普通计算机能计算一个带标号完全图的生成树个数，而文艺计算姬能计算一个带标号完全二分图的生成树个数。
　　更具体地，给定一个一边点数为n，另一边点数为m，共有n*m条边的带标号完全二分图K_{n,m}，计算姬能快速算出其生成树个数。
　　小W不知道计算姬算的对不对，你能帮助他吗？

Input

　　仅一行三个整数n,m,p，表示给出的完全二分图K_{n,m}

Output

　　仅一行一个整数，表示完全二分图K_{n,m}的生成树个数，答案需要模p。

Sample Input

　　2 3 7

Sample Output

　　5

HINT

　　1 <= n,m,p <= 10^18

Main idea

　　询问带标号的完全二分图生成树个数。

Solution

　　我们简单地用矩阵树定理以及各种公式（用观察法得到）证明出答案等于：

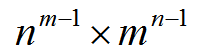
　　然后我们暴力写一个快速幂即可，又由于p<=10^18，两数相乘会爆long long，我们再用类似快速幂的方法写一个慢速乘来做乘法即可。

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef unsigned long long ull;
 typedef long long s64;

 s64 n,m,MOD;

 s64 Slowcheng(s64 a,s64 b)
 {
         s64 res=;
         while(b)
         {
             if(b&) res=((ull)res+a)%MOD;
             a=((ull)a+a)%MOD;
             b>>=;
         }
         return res;
 }

 s64 Quickpow(s64 a,s64 b)
 {
         s64 res=;
         while(b)
         {
             if(b&) res=(ull)Slowcheng(res,a);
             a=(ull)Slowcheng(a,a);
             b>>=;
         }
         return res;
 }

 int main()
 {
         cin>>n>>m>>MOD;
         printf("%lld",     Slowcheng(Quickpow(n,m-) , Quickpow(m,n-)));
 }