BFS搜索

参考博客：【算法入门】广度/宽度优先搜索(BFS)

适用问题：一个解/最优解

重点：我们怎么运用队列？怎么记录路径？

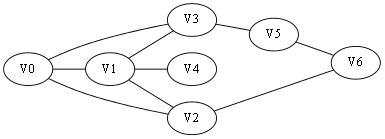
假设我们要找寻一条从V0到V6的最短路径。（明显看出这条最短路径就是V0->V2->V6）

BFS搜索：首先看跟V0直接连接的节点V1、V2、V3，发现没有V6；进而再看跟V1、V2、V3直接连接的节点分别是：{V0, V4}、{V0, V1, V6}、{V0, V1, V5}（这里画删除线的意思是那些顶点在我们刚刚的搜索过程中已经找过了，我们不需要重新回头再看它们了）；这时候我们从V2的连通节点集中找到了V6，那说明我们找到了这条V0到V6的最短路径：V0->V2->V6。（虽然你再进一步搜索V5的连接节点集合后会找到另一条路径V0->V3->V5->V6，但显然它不是最短路径。当然找到解后就不再需要搜索了，上一句的假设只能是假设，连实践都做不到。）

你会看到这里有点像辐射形状的搜索方式，从一个节点，向其旁边节点传递病毒，就这样一层一层的传递辐射下去，知道目标节点被辐射中了，此时就已经找到了从起点到终点的路径。

我们采用示例图来说明这个过程，在搜索的过程中，初始所有节点是白色（代表了所有点都还没开始搜索），把起点V0标志成灰色（表示即将辐射V0），下一步搜索的时候，我们把所有的灰色节点访问一次，然后将其变成黑色（表示已经被辐射过了），进而再将他们所能到达的节点标志成灰色（因为那些节点是下一步搜索的目标点了），但是这里有个判断，就像刚刚的例子，当访问到V1节点的时候，它的下一个节点应该是V0和V4，但是V0已经在前面被染成黑色了，所以不会将它染灰色。这样持续下去，直到目标节点V6被染灰色，说明了下一步就到终点了，没必要再搜索（染色）其他节点了，此时可以结束搜索了，整个搜索就结束了。然后根据搜索过程，反过来把最短路径找出来，图3-1中把最终路径上的节点标志成绿色。

初始全部都是白色（未访问）

即将搜索起点V0（灰色）

已搜索V0，即将搜索V1、V2、V3

……终点V6被染灰色，终止

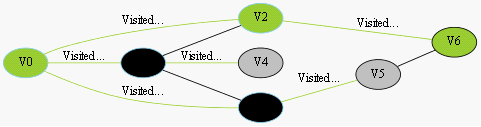找到最短路径

　　　　　　　　　图3-1  寻找V0到V6的过程

【BFS搜索流程图】

【队列使用示例】

以如下图的无向图G4为例，进行图的宽度优先搜索：

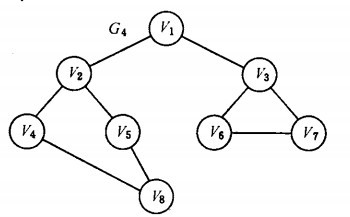
假设从顶点v₁出发进行搜索，首先访问v₁和v₁的邻接点v₂和v₃，然后依次访问v₂的邻接点v₄和v₅及v₃的邻接点v₆和v₇，最后访问v₄的邻接点v₈。由于这些顶点的邻接点均已被访问，并且图中所有顶点都被访问，由些完成了图的遍历。得到的顶点访问序列为：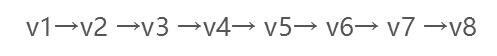

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

int n, m;
int graph[105][105];
bool vis[105];
queue<int> q;

void init()
{
    memset(map,0,sizeof(map));
    memset(vis,0,sizeof(vis));
    while(!q.empty())   q.pop();
}

void BFS(int u)
{
    vis[u] = 1;
    cout<<u<<"\t";
    q.push(u);　　　　　　　　　　　　　　　　　　//p1
    while(!q.empty()){　　　　　　　　　　　　　　//p2
        int p = q.front();　　　　　　　　　　　　//p3
        q.pop();　　　　　　　　　　　　　　　　　　//p4
        for(int i=1;i<=n;i++){
            if(!vis[i] && graph[p][i]==1){
                q.push(i);　　　　　　　　　　//p5
                cout<<i<<"\t";
                vis[i] = 1;
            }
        }
    }
}

void read()
{
    init();
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int u, v;
        cin>>u>>v;
        graph[u][v] = graph[v][u] = 1;
    }
    for(int i=1;i<=n;i++){
        if(!vis[i])
            BFS(i);
    }
    cout<<endl;
}

int main()
{
    read();
    return 0;
}