最短路径——Bellman-Ford算法以及SPFA算法

说完dijkstra算法，有提到过朴素dij算法无法处理负权边的情况，这里就需要用到Bellman-Ford算法，抛弃贪心的想法，牺牲时间的基础上，换取负权有向图的处理正确。

---

单源最短路径

Bellman-Ford算法

思维

一张有向图，有n个点，m条边，用dis[]数组保存源点到各点的最短距离，可以通过对边进行n-1次的遍历，当其满足dis[v]>dis[u]+w的时候，就对其进行松弛更新，重复n-1次以后就能得到答案，如果n-1次以后还能继续更新，则可以判断图中出现了负权环，思路非常简短。

---

举例演算

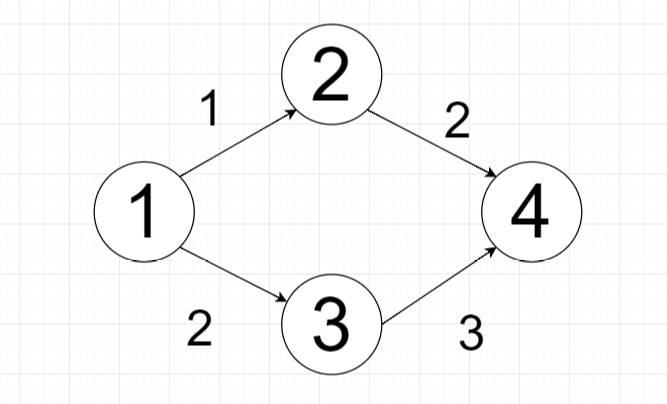
我们依然设置1为源点，为了直观展现算法思路，设定边的输入顺序如下:

2 4 2

3 4 3

1 2 1

1 3 2

次序	dis[1]	dis[2]	dis[3]	dis[4]
初始化	0	∞	∞	∞
1	0	1	2	∞
2	0	1	2	3
3	0	1	2	3

第一次遍历中，由于点2和点4的距离都是无限大，无法松弛，点3和点4同理。点1和点2，点1和点3符合松弛条件，更新。第二次遍历中，点2和点4就可以松弛更新了，点3和点4也是同理。第三次遍历是一次无用遍历，所有边都已经松弛过了。

由此也能够看出，其实不用进行n-1的遍历就可以得到答案了，可以加入一个bool标记来提前结束这个循环过程。

---

代码实现

时间复杂度O(NM)

#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>

using namespace std;

const int MAX = 1000;

int u[MAX], v[MAX], w[MAX], dis[MAX];
int n, m;

void Ford(int s) {
	for (int i = 1; i <= n; i++) dis[i] = 0x7fffffff;
	dis[s] = 0;
	for (int i = 0; i < n - 1; i++) {
		bool check = 0;
		for (int j = 0; j < m; j++) {
			if ((dis[v[j]] >= 0x7fffffff) && (dis[u[j]] >= 0x7fffffff)) continue;
			else {
				if (dis[v[j]] > dis[u[j]] + w[j]) {
					dis[v[j]] = dis[u[j]] + w[j];
					check = 1;
				}
			}
		}
		if (!check) break;
	}
}

int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++) cin >> u[i] >> v[i] >> w[i];
	int x;
	cin >> x;
	Ford(x);
	cout << endl;
	for (int i = 1; i <= n; i++) {
		if (dis[i] > 100000) cout << "none" << " ";
		else cout << dis[i] << " ";
	}
	cout << endl;
	return 0;
}

---

SPFA算法

思维

SPFA算法就是用双端队列优化过的Bellman-Ford算法，初始时将源点加入队列。每次选出队首结点，对其的所有出边进行松弛更新，更新成功的点加入队列，同一个结点可能被多次更新，但是同一个结点只能在同时在队列中出现一个，重复这个操作直到队列为空。这里其实有点像是上一篇dij堆优化代码的思路了。只是缺少了贪心。

---

代码实现

#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
sing namespace std;

const int MAX = 1000;

int h[MAX * 2], nxt[MAX * 2], to[MAX * 2], co[MAX * 2], dis[MAX], k = 0, book[MAX];
int n, m;

void insert(int u, int v, int c) {
	nxt[++k] = h[u];
	h[u] = k;
	to[k] = v;
	co[k] = c;
}

void SPFA(int s) {
	for (int i = 1; i <= n; i++) {
		book[i] = 0;
		dis[i] = 0x7fffffff;
	}
	queue<int> que;
	que.push(s);
	dis[s] = 0;
	book[s] = 1;
	while (!que.empty()) {
		int cur = que.front();
		for (int i = h[cur]; i; i = nxt[i]) {

			if (dis[to[i]] > dis[cur] + co[i]) {
				dis[to[i]] = dis[cur] + co[i];
				if (book[to[i]] == 0) {
					que.push(to[i]);
					book[to[i]] = 1;
				}
			}
		}
		que.pop();
		book[cur] = 0;
	}
}

int main() {
	cin >> n >> m;
	int u, v, w;
	for (int i = 0; i < m; i++) {
		cin >> u >> v >> w;
		insert(u, v, w);
	}
	int x;
	cin >> x;
	SPFA(x);
	for (int i = 1; i <= n; i++) {
		if (dis[i] > 100000) cout << "none" << " ";
		else cout << dis[i] << " ";
	}
	cout << endl;
	return 0;
}