原文:Matlab随笔之分段线性函数化为线性规划

eg：

10x,            0<=x<=500

c(x)=1000+8x,    500<=x<=1000

3000+6x,    1000<=x<=1500

解法一：

可引入0-1变量，令z1=1，z2=1,z3=1分别表示0<=x<=500,500<=x<=1000,1000<=x<=1500,则

500z2<=x1<=500z1,

500z3<=x2<=500z2,

x3<=500z3,

c(x)=10x1+8x2+6x3

解法二：（更具一般性）

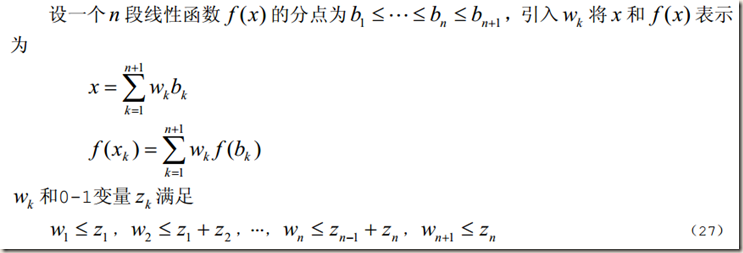
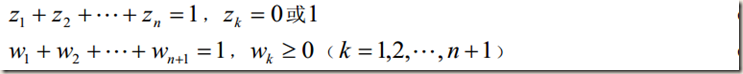
Matlab随笔之分段线性函数化为线性规划的更多相关文章

  1. Matlab随笔之线性规划

    原文:Matlab随笔之线性规划   LP(Linear programming,线性规划)是一种优化方法,在优化问题中目标函数和约束函数均为向量变量的线性函数,LP问题可描述为:min xs.t. ...

  2. Matlab随笔之插值与拟合（上）

    原文:Matlab随笔之插值与拟合(上) 1.拉格朗日插值 新建如下函数: function y=lagrange(x0,y0,x) %拉格朗日插值函数 %n 个节点数据以数组 x0, y0 输入(注 ...

  3. Matlab随笔之插值与拟合（下）

    原文:Matlab随笔之插值与拟合(下) 1.二维插值之插值节点为网格节点 已知m x n个节点:(xi,yj,zij)(i=1…m,j=1…n),且xi,yi递增.求(x,y)处的插值z. Matl ...

  4. relu函数为分段线性函数，为什么会增加非线性元素

    relu函数为分段线性函数,为什么会增加非线性元素 我们知道激活函数的作用就是为了为神经网络增加非线性因素,使其可以拟合任意的函数.那么relu在大于的时候就是线性函数,如果我们的输出值一直是在大于0 ...

  5. Matlab随笔之矩阵入门知识

    原文:Matlab随笔之矩阵入门知识 直接输入法创建矩阵 – 矩阵的所有元素必须放在方括号“[ ]”内: – 矩阵列元素之间必须用逗号“,”或空格隔开,每行必须用“;”隔开 – 矩阵元素可以是任何不含 ...

  6. Matlab随笔之画图函数总结

    原文:Matlab随笔之画图函数总结 MATLAB函数画图 MATLAB不但擅长於矩阵相关的数值运算,也适合用在各种科学目视表示(Scientific visualization).本节将介绍MATL ...

  7. Matlab随笔之指派问题的整数规划

    原文:Matlab随笔之指派问题的整数规划 注:除了指派问题外,一般的整数规划问题无法直接利用Matlab函数,必须Matlab编程实现分支定界法和割平面解法. 常用Lingo等专用软件求解整数规划问 ...

  8. Matlab随笔之求解线性方程

    原文:Matlab随笔之求解线性方程 理论知识补充: %矩阵除分为矩阵右除和矩阵左除. %矩阵右除的运算符号为“/”,设A,B为两个矩阵,则“A/B”是指方程X*B=A的解矩阵X. %矩阵A和B的列数 ...

  9. Matlab随笔之判别分析

    原文:Matlab随笔之判别分析 从概率论角度,判别分析是根据所给样本数据,对所给的未分类数据进行分类. 如下表,已知有t个样本数据,每个数据关于n个量化特征有一个值,又已知该样本数据的分类,据此,求 ...

随机推荐

  1. [Math Processing Error] 问题的解决（F5刷新页面与 Ctrl/Shift + F5 刷新页面的区别）

    Why is [Math Processing Error] all over the place today? 当打开某页面出现 [Math Processing Error],一般表示 MathJ ...

  2. [Angular2 Router] Setup page title with Router events

    Article import 'rxjs/add/operator/filter'; import 'rxjs/add/operator/map'; import 'rxjs/add/operator ...

  3. swift学习第八天：元组

    元组的介绍 元组是Swift中特有的,OC中并没有相关类型 它是什么呢? 它是一种数据结构,在数学中应用广泛 类似于数组或者字典 可以用于定义一组数据 组成元组类型的数据可以称为“元素” 元组的定义 ...

  4. Nutch+Hadoop集群搭建 分类： H3_NUTCH 2015-01-18 10:55 362人阅读 评论(0) 收藏

    转载自:http://www.open-open.com/lib/view/open1328670771405.html 1.Apache Nutch    Apache Nutch是一个用于网络搜索 ...

  5. Web全栈工程师修养

    全栈工程师现在是个很热的话题,如何定义全栈工程师?在著名的问答网站Quora上有人提出了这个问题,其中一个获得了高票的回答是: 全栈工程师是指,一个能处理数据库.服务器.系统工程和客户端的所有工作的工 ...

  6. ssion机制详解

    ssion机制详解   ref:http://justsee.iteye.com/blog/1570652 虽然session机制在web应用程序中被采用已经很长时间了,但是仍然有很多人不清楚sess ...

  7. signed 与 unsigned 有符号和无符号数

    unsigned int a = 0; unsigned int b = -1; // b 为 0xffffffff unsigned int c = a - 1; // c 为 0xffffffff

  8. [DevExpress]DevExpress 中 汉化包 汉化方法

    第一步: 在Debug 下加入 zh-CN 汉化包(自行下载) 第二步: 在 Program.cs中加入下面代码 : System.Threading.Thread.CurrentThread.Cur ...

  9. js进阶 9-9 html控件如何实现回车键切换焦点

    js进阶 9-9 html控件如何实现回车键切换焦点 一.总结 一句话总结:在onkeydown事件中判断event对象的键位码,然后focus事件. 二.js进阶 9-9 html控件如何实现回车键 ...

  10. 64位Oracle11g自带的sqldevelper无法启动

    原因:选择的jdk有问题 解决方法:由于Oracle自带的Sqldeveloper只支持32位的java运行环境,如果本机安装64位jdk,需要手动更改SqlDeveloper路径到32位的jdk即可 ...