Spark MLlib架构解析（含分类算法、回归算法、聚类算法和协同过滤）

Spark MLlib架构解析

• MLlib的底层基础解析
• MLlib的算法库分析
  • 　　分类算法　
  • 　　回归算法
  • 聚类算法
  • 协同过滤
• MLlib的实用程序分析

从架构图可以看出MLlib主要包含三个部分：

• 底层基础：包括Spark的运行库、矩阵库和向量库；
• 算法库：包含广义线性模型、推荐系统、聚类、决策树和评估的算法；
• 实用程序：包括测试数据的生成、外部数据的读入等功能。

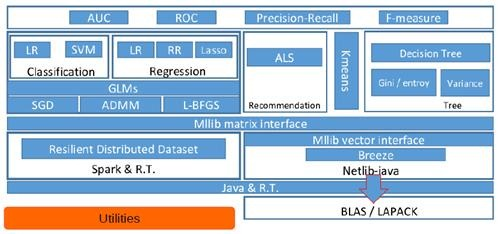
MLlib的底层基础解析

　　底层基础部分主要包括向量接口和矩阵接口，这两种接口都会使用Scala语言基于Netlib和BLAS/LAPACK开发的线性代数库Breeze。

　　MLlib支持本地的密集向量和稀疏向量，并且支持标量向量。

　　MLlib同时支持本地矩阵和分布式矩阵，支持的分布式矩阵分为RowMatrix、IndexedRowMatrix、CoordinateMatrix等。

　　关于密集型和稀疏型的向量Vector的示例如下所示。

　　　　　　

　　　　　　　　　　　　　　　　

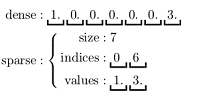
　　疏矩阵在含有大量非零元素的向量Vector计算中会节省大量的空间并大幅度提高计算速度，如下图所示。

　　　　　　　　　　　　 

　　标量LabledPoint在实际中也被大量使用，例如判断邮件是否为垃圾邮件时就可以使用类似于以下的代码：

　　　　　　　　　　　　　　

　　可以把表示为1.0的判断为正常邮件，而表示为0.0则作为垃圾邮件来看待。

　　对于矩阵Matrix而言，本地模式的矩阵如下所示。

　　　　　　  

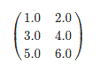
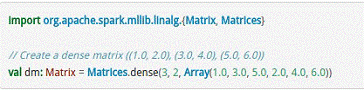
　　分布式矩阵如下所示。

　　　　　　　　

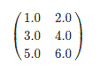
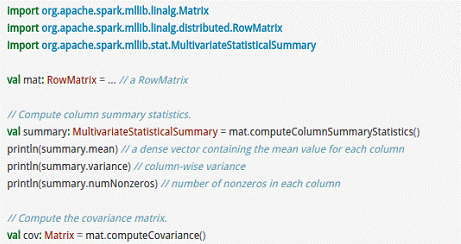
　　RowMatrix直接通过RDD[Vector]来定义并可以用来统计平均数、方差、协同方差等：

　　　　　　 

　　　　　　

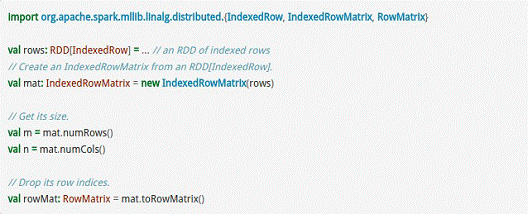
　　而IndexedRowMatrix是带有索引的Matrix，但其可以通过toRowMatrix方法来转换为RowMatrix，从而利用其统计功能，代码示例如下所示。

　　　　　　

　　CoordinateMatrix常用于稀疏性比较高的计算中，是由RDD[MatrixEntry]来构建的，MatrixEntry是一个Tuple类型的元素，其中包含行、列和元素值，代码示例如下所示：

　　　　　　　　　　

MLlib的算法库分析

　　下图是MLlib算法库的核心内容。

　　　　　　　　

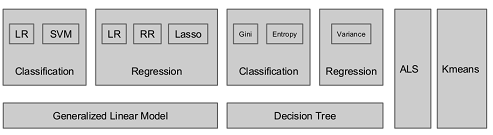
　　在这里我们分析一些Spark中常用的算法：

　　

　　1) 分类算法

　　分类算法属于监督式学习，使用类标签已知的样本建立一个分类函数或分类模型，应用分类模型，能把数据库中的类标签未知的数据进行归类。分类在数据挖掘中是一项重要的任务，目前在商业上应用最多，常见的典型应用场景有流失预测、精确营销、客户获取、个性偏好等。MLlib 目前支持分类算法有：逻辑回归、支持向量机、朴素贝叶斯和决策树。

　　案例：导入训练数据集，然后在训练集上执行训练算法，最后在所得模型上进行预测并计算训练误差。

import org.apache.spark.SparkContext
import org.apache.spark.mllib.classification.SVMWithSGD
import org.apache.spark.mllib.regression.LabeledPoint

// 加载和解析数据文件
val data = sc.textFile("mllib/data/sample_svm_data.txt")
val parsedData = data.map { line =>
  val parts = line.split(' ')
  LabeledPoint(parts().toDouble, parts.tail.map(x => x.toDouble).toArray)
}

// 设置迭代次数并进行进行训练
val numIterations =
val model = SVMWithSGD.train(parsedData, numIterations)

// 统计分类错误的样本比例
val labelAndPreds = parsedData.map { point =>
val prediction = model.predict(point.features)
(point.label, prediction)
}
val trainErr = labelAndPreds.filter(r => r._1 != r._2).count.toDouble / parsedData.count
println("Training Error = " + trainErr)

　　

　　2) 回归算法

　　回归算法属于监督式学习，每个个体都有一个与之相关联的实数标签，并且我们希望在给出用于表示这些实体的数值特征后，所预测出的标签值可以尽可能接近实际值。MLlib 目前支持回归算法有：线性回归、岭回归、Lasso和决策树。

　　案例：导入训练数据集，将其解析为带标签点的RDD，使用 LinearRegressionWithSGD 算法建立一个简单的线性模型来预测标签的值，最后计算均方差来评估预测值与实际值的吻合度。

import org.apache.spark.mllib.regression.LinearRegressionWithSGD
import org.apache.spark.mllib.regression.LabeledPoint

// 加载和解析数据文件
val data = sc.textFile("mllib/data/ridge-data/lpsa.data")
val parsedData = data.map { line =>
  val parts = line.split(',')
  LabeledPoint(parts().toDouble, parts().split(' ').map(x => x.toDouble).toArray)
}

//设置迭代次数并进行训练
val numIterations =
val model = LinearRegressionWithSGD.train(parsedData, numIterations)

// 统计回归错误的样本比例
val valuesAndPreds = parsedData.map { point =>
val prediction = model.predict(point.features)
(point.label, prediction)
}
val MSE = valuesAndPreds.map{ case(v, p) => math.pow((v - p), )}.reduce(_ + _)/valuesAndPreds.count
println("training Mean Squared Error = " + MSE)

　　

　　3)  聚类算法

　　聚类算法属于非监督式学习，通常被用于探索性的分析，是根据“物以类聚”的原理，将本身没有类别的样本聚集成不同的组，这样的一组数据对象的集合叫做簇，并且对每一个这样的簇进行描述的过程。它的目的是使得属于同一簇的样本之间应该彼此相似，而不同簇的样本应该足够不相似，常见的典型应用场景有客户细分、客户研究、市场细分、价值评估。MLlib 目前支持广泛使用的KMmeans聚类算法。

　　案例：导入训练数据集，使用 KMeans 对象来将数据聚类到两个类簇当中，所需的类簇个数会被传递到算法中，然后计算集内均方差总和(WSSSE)，可以通过增加类簇的个数 k 来减小误差。 实际上，最优的类簇数通常是 1，因为这一点通常是WSSSE图中的 “低谷点”。

import org.apache.spark.mllib.clustering.KMeans

// 加载和解析数据文件
val data = sc.textFile("kmeans_data.txt")
val parsedData = data.map( _.split(' ').map(_.toDouble))
// 设置迭代次数、类簇的个数
val numIterations =
val numClusters = 

// 进行训练
val clusters = KMeans.train(parsedData, numClusters, numIterations)

// 统计聚类错误的样本比例
val WSSSE = clusters.computeCost(parsedData)
println("Within Set Sum of Squared Errors = " + WSSSE)

　　4) 协同过滤

　　协同过滤常被应用于推荐系统，这些技术旨在补充用户-商品关联矩阵中所缺失的部分。MLlib当前支持基于模型的协同过滤，其中用户和商品通过一小组隐语义因子进行表达，并且这些因子也用于预测缺失的元素。

　　案例：导入训练数据集，数据每一行由一个用户、一个商品和相应的评分组成。假设评分是显性的，使用默认的ALS.train()方法，通过计算预测出的评分的均方差来评估这个推荐模型。

import org.apache.spark.mllib.recommendation.ALS
import org.apache.spark.mllib.recommendation.Rating

// 加载和解析数据文件
val data = sc.textFile("mllib/data/als/test.data")
val ratings = data.map(_.split(',') match {
case Array(user, item, rate) => Rating(user.toInt, item.toInt, rate.toDouble)
})

// 设置迭代次数
val numIterations =
val model = ALS.train(ratings, , , 0.01)

// 对推荐模型进行评分
val usersProducts = ratings.map{ case Rating(user, product, rate) => (user, product)}
val predictions = model.predict(usersProducts).map{
case Rating(user, product, rate) => ((user, product), rate)
}
val ratesAndPreds = ratings.map{
case Rating(user, product, rate) => ((user, product), rate)
}.join(predictions)
val MSE = ratesAndPreds.map{
case ((user, product), (r1, r2)) => math.pow((r1- r2), )
}.reduce(_ + _)/ratesAndPreds.count
println("Mean Squared Error = " + MSE)

MLlib的实用程序分析

　　实用程序部分包括数据的验证器、Label的二元和多元的分析器、多种数据生成器、数据加载器。