Codeforces Round #277 (Div. 2) D. Valid Sets DP

D. Valid Sets

 

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

1. S is non-empty.
2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
3. .

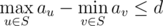Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo 1000000007(109 + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a1, a2, ..., an(1 ≤ ai ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Sample test(s)

input

1 4
2 1 3 2
1 2
1 3
3 4

output

8

 

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4} is not valid, because the third condition isn't satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

题意：给你一个n点的树，和每个点的权值，问你多少种子树满足(最大权值点-最小权值点)<=d

题解：定义dp[i]表示以i为最小权值根节点的子树方案数，注意维护此条件

于是答案就是  ∑dp[i] %mod (1<=i<=n);

///
#include<bits/stdc++.h>
using namespace std ;
typedef long long ll;
#define mem(a) memset(a,0,sizeof(a))
#define pb push_back
#define meminf(a) memset(a,127,sizeof(a));

inline ll read()
{
    ll x=,f=;char ch=getchar();
    while(ch<''||ch>''){
        if(ch=='-')f=-;ch=getchar();
    }
    while(ch>=''&&ch<=''){
        x=x*+ch-'';ch=getchar();
    }return x*f;
}
//****************************************
#define maxn 2000+50
#define mod 1000000007
#define inf 1000000007
int d,n,a[maxn],vis[maxn];
vector<int >G[maxn];
ll dp[maxn];//以i为最小根节点，的方案数
void dfs(int x,int pre){
   dp[x]=;vis[x]=;
   for(int i=;i<G[x].size();i++){
      if(!vis[G[x][i]]){
            if(a[G[x][i]]<a[pre]||a[G[x][i]]>a[pre]+d)continue;
            if(a[G[x][i]]==a[pre]&&G[x][i]<pre)continue;
            dfs(G[x][i],pre);
            dp[x]=(dp[x]*(dp[G[x][i]]+))%mod;
      }
   }
}

int main(){
    d=read(),n=read();
    for(int i=;i<=n;i++){
        scanf("%d",&a[i]);
    }int u,v;
    for(int i=;i<n;i++){
        scanf("%d%d",&u,&v);
        G[u].pb(v);G[v].pb(u);
    }ll ans=;
    for(int i=;i<=n;i++){
        mem(dp);mem(vis);
        dfs(i,i);
        ans=(ans+dp[i])%mod;
    }
    cout<<ans<<endl;
  return ;
}

代码