HDU4288：Coder(线段树单点更新版 && 暴力版)

Problem Description

In mathematics and computer science, an algorithm describes a set of procedures or instructions that define a procedure. The term has become increasing popular since the advent of cheap and reliable computers. Many companies now employ a single coder to write an algorithm that will replace many other employees. An added benefit to the employer is that the coder will also become redundant once their work is done.   ¹
You are now the signle coder, and have been assigned a new task writing code, since your boss would like to replace many other employees (and you when you become redundant once your task is complete).

Your code should be able to complete a task to replace these employees who do nothing all day but eating: make the digest sum.

By saying “digest sum” we study some properties of data. For the sake of simplicity, our data is a set of integers. Your code should give response to following operations:

1. add x – add the element x to the set;

2. del x – remove the element x from the set;

3. sum – find the digest sum of the set. The digest sum should be understood by

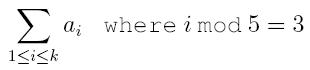
where the set S is written as {a
₁, a
₂, ... , a
_k} satisfying a
₁
 < a
₂
 < a
₃
 < ... < a
_k
 

Can you complete this task (and be then fired)?

------------------------------------------------------------------------------


¹
 See http://uncyclopedia.wikia.com/wiki/Algorithm

 

Input

There’re several test cases.

In each test case, the first line contains one integer N ( 1 <= N <= 10
⁵
 ), the number of operations to process.

Then following is n lines, each one containing one of three operations: “add x” or “del x” or “sum”.

You may assume that 1 <= x <= 10
⁹.

Please see the sample for detailed format.

For any “add x” it is guaranteed that x is not currently in the set just before this operation.

For any “del x” it is guaranteed that x must currently be in the set just before this operation.

Please process until EOF (End Of File).

 

Output

For each operation “sum” please print one line containing exactly one integer denoting the digest sum of the current set. Print 0 if the set is empty.

 

Sample Input

9
add 1
add 2
add 3
add 4
add 5
sum
add 6
del 3
sum
6
add 1
add 3
add 5
add 7
add 9
sum

 

Sample Output

3
4
5

Hint

C++ maybe run faster than G++ in this problem.

思路：这道题很明显是线段树的单点更新区间求和的问题，因为要求的是对５取余为３的所有数的和，我们可以将对５取余的５种情况进行离散化，而且这道题暴力也能过，不过时间几乎是踩线的。

先来暴力代码，这是老板大神的做法，真心碉堡了，暴力的精华在于要保持数组的有序性，只是时间比较长

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

int n;
int a[100005],len;
char str[10];
__int64 sum;

int main()
{
    int i,j,k;
    while(~scanf("%d",&n))
    {
        len = 0;
        while(n--)
        {
            scanf("%s",str);
            if(!strcmp(str,"add"))
            {
                scanf("%d",&k);
                for(i = len++; i>0; i--)//保持有序的插入
                {
                    if(a[i-1]>k)
                        a[i] = a[i-1];
                    else
                        break;
                }
                a[i] = k;
            }
            else if(!strcmp(str,"del"))
            {
                scanf("%d",&k);
                for(i = 0; i<len; i++)//找到删除的位置
                    if(a[i] == k)
                        break;
                for(; i<len; i++)//删除后后面的数前移
                    a[i] = a[i+1];
                len--;
            }
            else if(!strcmp(str,"sum"))
            {
                sum = 0;
                for(i = 2; i<len; i+=5)//所有队伍取余为3的和加起来
                    sum+=a[i];
                printf("%I64d\n",sum);
            }
        }
    }

    return 0;
}

然后是线段树的，时间方面大大减少了

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;

const int maxn = 500000+10;

int n,len,flag;
char str[maxn][10];
int num[maxn],s[maxn];

struct node
{
    int l,r,cnt;
    __int64 sum[5];//sum[i]保存与5模的各组和
} a[maxn<<2];

int bin(int k)
{
    int l = 0,r = len-1;
    while(l<=r)
    {
        int mid = (l+r)>>1;
        if(s[mid]<k)
            l = mid+1;
        else if(s[mid]>k)
            r = mid-1;
        else
            return mid;
    }
}

void init(int l,int r,int i)
{
    a[i].l = l;
    a[i].r = r;
    a[i].cnt = 0;
    memset(a[i].sum,0,sizeof(a[i].sum));
    if(l!=r)
    {
        int mid = (l+r)>>1;
        init(l,mid,2*i);
        init(mid+1,r,2*i+1);
    }
}

void add(int x)
{
    for(int i = 0; i<5; i++)
        a[x].sum[i] = a[x*2].sum[i]+a[x*2+1].sum[((i-a[x*2].cnt)%5+5)%5];//这个区间的和是左右子树同样余数的相加和，右子树要用序号减去左子树的个数对5取模后为了保持正数所以要+5再取模，所以是(i-a[x*2].cnt)%5+5
}

void insert(int i,int pos,int m)
{
    a[i].cnt+=2*flag-1;//区间内有几个数字
    if(a[i].l == a[i].r)
    {
        a[i].sum[0] = flag*m;//删除则此位清0，add则进行更新
        return;
    }
    int mid = (a[i].l+a[i].r)>>1;
    if(pos<=mid)
        insert(2*i,pos,m);
    else
        insert(2*i+1,pos,m);
    add(i);
}

int main()
{
    int i,pos;
    while(~scanf("%d",&n))
    {
        len = 0;
        for(i = 0; i<n; i++)
        {
            scanf("%s",str[i]);
            if(str[i][0] != 's')
            {
                scanf("%d",&num[i]);
                s[len++] = num[i];
            }
        }
        sort(s,s+len);
        len = unique(s,s+len)-s;//去重
        if(!len)
            memset(a[1].sum,0,sizeof(a[1].sum));
        else
            init(1,len,1);
        for(i = 0; i<n; i++)
        {
            if(str[i][0] == 'a')
            {
                flag = 1;
                pos = bin(num[i]);
                insert(1,pos,num[i]);
            }
            else if(str[i][0] == 'd')
            {
                flag = 0;
                int pos = bin(num[i]);
                insert(1,pos,num[i]);
            }
            else
                printf("%I64d\n",a[1].sum[2]);
        }
    }

    return 0;
}