NOIP 2008 立体图

洛谷 P1058 立体图

洛谷传送门

JDOJ 1541: [NOIP2008]立体图 T4

JDOJ传送门

题目描述

小渊是个聪明的孩子，他经常会给周围的小朋友们将写自己认为有趣的内容。最近，他准备给小朋友们讲解立体图，请你帮他画出立体图。

小渊有一块面积为m \times nm×n的矩形区域，上面有m \times nm×n个边长为11的格子，每个格子上堆了一些同样大小的积木（积木的长宽高都是11），小渊想请你打印出这些格子的立体图。我们定义每个积木为如下格式，并且不会做任何翻转旋转，只会严格以这一种形式摆放：

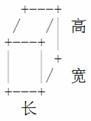
每个顶点用11个加号’++’表示，长用33个”-−”表示，宽用11个”/”，高用两个”|”表示。字符’++’,”-−”,”/”,”|”的ASCIIASCII码分别为4343，4545，4747，124124。字符’.’(ASCIIASCII码4646)需要作为背景输出，即立体图里的空白部分需要用’.’来代替。立体图的画法如下面的规则：

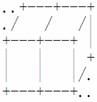
若两块积木左右相邻，图示为：

若两块积木上下相邻，图示为：

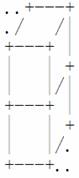
若两块积木前后相邻，图示为：

立体图中，定义位于第(m,1(m,1)的格子（即第mm行第11列的格子）上面自底向上的第一块积木（即最下面的一块积木）的左下角顶点为整张图最左下角的点。

输入格式

第一行有用空格隔开的22个整数mm和nn，表示有m \times nm×n个格子(1 \le m,n \le 50)(1≤m,n≤50)。

接下来的mm行，是一个m \times nm×n的矩阵，每行有nn个用空格隔开的整数，其中第ii行第jj列上的整数表示第ii行第jj列的个子上摞有多少个积木（1 \le1≤每个格子上的积木数\le 100≤100）。

输出格式

输出包含题目要求的立体图，是一个KK行LL列的字符串矩阵，其中KK和LL表示最少需要KK行LL列才能按规定输出立体图。

输入输出样例

输入 #1复制

输出 #1复制

说明/提示

NOIP2008普及组第四题

题解：

一道非常好的模拟大题。

这道题乍一看给人一种无从下手的感觉，但是理清思路，明白步骤之后就非常好做。

首先我们明白，这道题的实质就是打印一张符合要求的立方体视图。

所以我们一定要明白这个东西的长宽。

长度k，需要被不断更新，由输入而定。

宽度l只由n,m决定，其公式为4m（一个块的底边长5（需要减一））+2n(一个块的宽度映射下来是2)，最后还要加上1。

（不明白的看图示）

宽度k是同理的。

然后我们考虑用数组的形式输出，先把要输出的内容存到一个数组里，最后直接打印k行l列的数组就可以了/

初始化的时候要置成“·”

然后就是要放正方体，放正方体的时候有这么几个难点：首先，怎么打印正方体，其次，怎么考虑覆盖的问题（可以理解成遮掩）。

我们把每一个正方体打进一个表里（解决问题1）

然后从后往前放正方体（覆盖的话就直接覆盖掉了）

然后我们得出AC代码。

#include<cstdio>
#include<algorithm>
using namespace std;
int n,m,k,l,x,y;
char block[6][8]=
{
    "..+---+",
    "./   /|",
    "+---+ |",
    "|   | +",
    "|   |/.",
    "+---+..",
};
int a[55][55];
char map[550][550];
void init(int x,int y)
{
    for(int i=0;i<6;i++)
        for(int j=0;j<7;j++)
            if(block[6-i-1][j]!='.')
                map[x-i][y+j]=block[6-i-1][j];
}
int main()
{
    scanf("%d%d",&n,&m);
    l=4*m+2*n+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
            k=max(k,a[i][j]*3+2*(n-i+1)+1);
        }
    for(int i=1;i<=k;i++)
        for(int j=1;j<=l;j++)
            map[i][j]='.';
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            x=k-2*(n-i);
            y=2*(n-i)+4*(j-1)+1;
            while(a[i][j]--)
            {
                init(x,y);
                x-=3;
            }
        }
    for(int i=1;i<=k;i++)
    {
        for(int j=1;j<=l;j++)
            printf("%c",map[i][j]);
        printf("\n");
    }
    return 0;
}