Python - 实现矩阵转置

有个朋友提出了一个问题：手头上现在有一个二维列表，比如[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]，现在要把该二维列表变成为[[1, 4, 7, 10], [2, 5, 8, 11], [3, 6, 9, 12]]。

其实不动脑筋的话，用二重循环很容易写出来：

#! /usr/bin/env python3
# -*- coding:utf-8 -*-

# Author   : mayi
# Blog     : http://www.cnblogs.com/mayi0312/
# Date     : 2019/4/26
# Name     : test01
# Software : PyCharm
# Note     : 用于实现实现矩阵（二重列表）转置

def trans(l):
    a = [[] for i in l[0]]
    for i in l:
        for j in range(len(i)):
            a[j].append(i[j])

    return a

# 主函数
def main():
    l1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]

    l2 = trans(l1)
    print(l1) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
    print(l2) # [[1, 4, 7, 10], [2, 5, 8, 11], [3, 6, 9, 12]]

# 入口函数
if __name__ == '__main__':
    main()

然而不管怎么看这种代码都很丑。

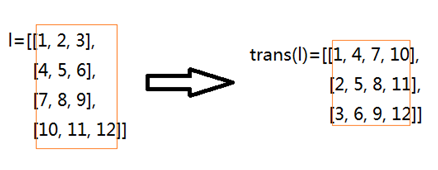
如上图：这种转置矩阵的即时感是怎么回事？

没错，这个问题的本质就是求解转置矩阵。于是就简单了，还是用个不动脑筋的办法：

#! /usr/bin/env python3
# -*- coding:utf-8 -*-

# Author   : mayi
# Blog     : http://www.cnblogs.com/mayi0312/
# Date     : 2019/4/26
# Name     : test01
# Software : PyCharm
# Note     : 用于实现实现矩阵（二重列表）转置

def trans(l):
    for i in range(len(l)):
        for j in range(i):
            l[i][j], l[j][i] = l[j][i], l[i][j]

    return l

# 主函数
def main():
    l1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

    l2 = trans(l1)
    print(l1) # [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
    print(l2) # [[1, 4, 7], [2, 5, 8], [3, 6, 9]]

# 入口函数
if __name__ == '__main__':
    main()

其实上面代码还是有点bug，看起来是好用的，然而用这种方法矩阵要求行列长度相同才行。

最后，我们想起了zip。zip的本质就是这样的，取出列表中的对应位置的元素，组成新列表，正是这个题目要做的。

所以最终，这个题目（转置矩阵）的Python解法就相当奇妙了：

#! /usr/bin/env python3
# -*- coding:utf-8 -*-

# Author   : mayi
# Blog     : http://www.cnblogs.com/mayi0312/
# Date     : 2019/4/26
# Name     : test01
# Software : PyCharm
# Note     : 用于实现实现矩阵（二重列表）转置

def trans(l):
    l = zip(*l)
    l = [list(i) for i in l]

    return l

# 主函数
def main():
    l1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]

    l2 = trans(l1)
    print(l1) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
    print(list(l2)) # [[1, 4, 7, 10], [2, 5, 8, 11], [3, 6, 9, 12]]

# 入口函数
if __name__ == '__main__':
    main()