TreeMap 还能排序？分析下源码就明白了

Java 中的 Map 是一种键值对映射，又被称为符号表或字典的数据结构，通常使用哈希表来实现，但也可使用二叉查找树、红黑树实现。

• HashMap 基于哈希表，但迭代时不是插入顺序
• LinkedHashMap 扩展了 HashMap，维护了一个贯穿所有元素的双向链表，保证按插入顺序迭代
• TreeMap 基于红黑树，保证键的有序性，迭代时按键大小的排序顺序

这里就来分析下 TreeMap 的实现。基于红黑树，就意味着结点的增删改查都能在 O(lgn) 时间复杂度内完成，如果按树的中序遍历就能得到一个按 键-key 大小排序的序列。

在看本文之前，建议看一下《红黑树这个数据结构，让你又爱又恨？看了这篇，妥妥的征服它》对红黑树的分析，理解了红黑树，你会发现 TreeMap 如此简单。

基本结构

TreeMap 的继承结构如下，其中包含了一些关键字段和方法：

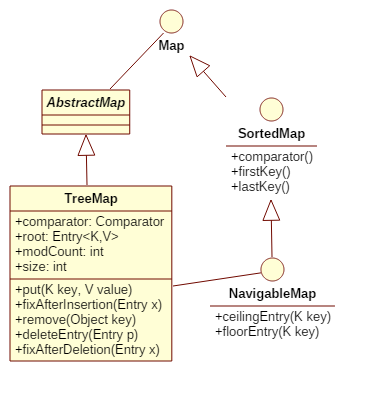
其中，相关字段的意义是：

• Comparator - 不为空，那么就用它维持 key-键 的有序，否则使用 key-键 的自然顺序
• size - 记录树中结点的个数
• modCount - 记录树结构变化次数，用于迭代器的快速失败

另一个字段是 Entry<K,V> root ，它表示根结点，初始为空，树结点的结构定义如下：

static final class Entry<K,V> implements Map.Entry<K,V> {
  K key;
  V value;
  Entry<K,V> left;  // 左孩子结点
  Entry<K,V> right; // 右孩子结点
  Entry<K,V> parent; // 父结点
  // 默认结点为黑色（在平衡操作时会先变成红色）
  boolean color = BLACK;

  // 创建一个无孩子的，黑色的结点
  Entry(K key, V value, Entry<K,V> parent) { ... }
  ...
}

TreeMap 是按照算法导论（CLR）的描述实现的，但略有不同，它没有使用隐形叶子结点 NIL，而是定义了一组访问方法来正确处理 NULL 叶子节点 的问题，用于避免在主算法中因检查空叶子结点引起的混乱，方法如下：

• colorOf(Entry<K,V> p): 返回结点颜色，如果为空返回黑色
• parentOf(Entry<K,V> p): 返回父结点的引用，根结点则返回 null
• setColor(Entry<K,V> p, boolean c): 设置结点颜色
• leftOf(Entry<K,V> p): 返回左孩子结点
• rightOf(Entry<K,V> p): 返回右孩子结点
• rotateLeft(Entry<K,V> p): 将结点 P 左旋转
• rotateRight(Entry<K,V> p): 将结点 P 右旋转
• fixAfterInsertion(Entry<K,V> x): 插入结点后的回调方法，重新平衡
• fixAfterDeletion(Entry<K,V> x): 删除结点后的回调方法，重新平衡

这些方法基本上都能见名知意，其中有点绕的就是树旋转的代码，代码实现如下：

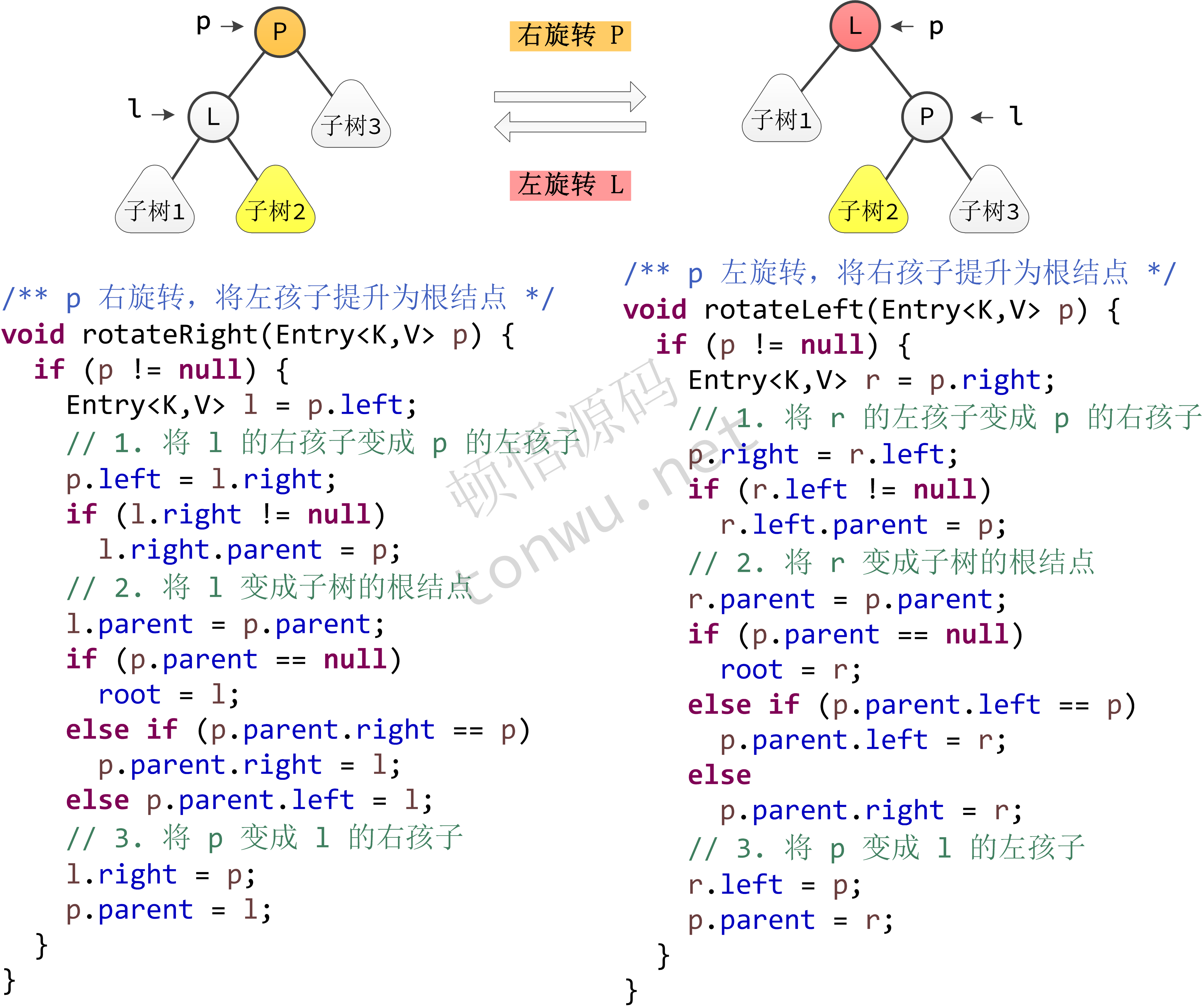
插入

结点的插入可能会打破红黑树的平衡，需要做旋转和颜色变换的调整。假设待插入结点为 N，P 是 N 的父结点，G 是 N 的祖父结点，U 是 N 的叔叔结点（即父结点的兄弟结点），那么红黑树有以下几种插入情况：

1. N 是根结点，即红黑树的第一个结点
2. N 的父结点（P）为黑色
3. P 是红色的（不是根结点），它的兄弟结点 U 也是红色的
4. P 为红色，而 U 为黑色
   
   4.1 P 左（右）孩子 N 右（左）孩子
   
   4.2 P 左（右）孩子 N 左（右）孩子

以上情况的分析可查看本文开头的文章链接，现在来看下 TreeMap 的 put 方法的实现：

public V put(K key, V value) {
  Entry<K,V> t = root;
  // 情况 1 - 空树，直接插入作为根结点
  if (t == null) {
    compare(key, key); // type (and possibly null) check
    root = new Entry<>(key, value, null);
    size = 1;
    modCount++;
    return null;
  }
  int cmp;
  Entry<K,V> parent;
  // split comparator and comparable paths
  Comparator<? super K> cpr = comparator;
  if (cpr != null) { // 使用 comparator 比较大小
    do { // 根据 key 的大小找到插入位置
      parent = t;
      cmp = cpr.compare(key, t.key);
      if (cmp < 0) t = t.left;
      else if (cmp > 0) t = t.right;
      else // 如果有相等的 key 直接设置 value 并返回
        return t.setValue(value);
    } while (t != null);
  }
  else {// 使用 key 的自然顺序
    if (key == null) throw new NullPointerException();
    @SuppressWarnings("unchecked")
    Comparable<? super K> k = (Comparable<? super K>) key;
    do {
      parent = t;
      cmp = k.compareTo(t.key);
      if (cmp < 0) t = t.left;
      else if (cmp > 0) t = t.right;
      else return t.setValue(value);
    } while (t != null);
  } // 新建一个结点插入
  Entry<K,V>e = new Entry<>(key, value, parent);
  if (cmp < 0) parent.left = e;
  else parent.right = e;
  fixAfterInsertion(e);// 可能会打破平衡，调整树结构
  size++;
  modCount++;
  return null;
}

put 方法比较简单，就是根据 key 的大小，递归的判断插入左子树还是右子树，比较复杂操作在于插入后重新平衡的调整，核心代码如下：

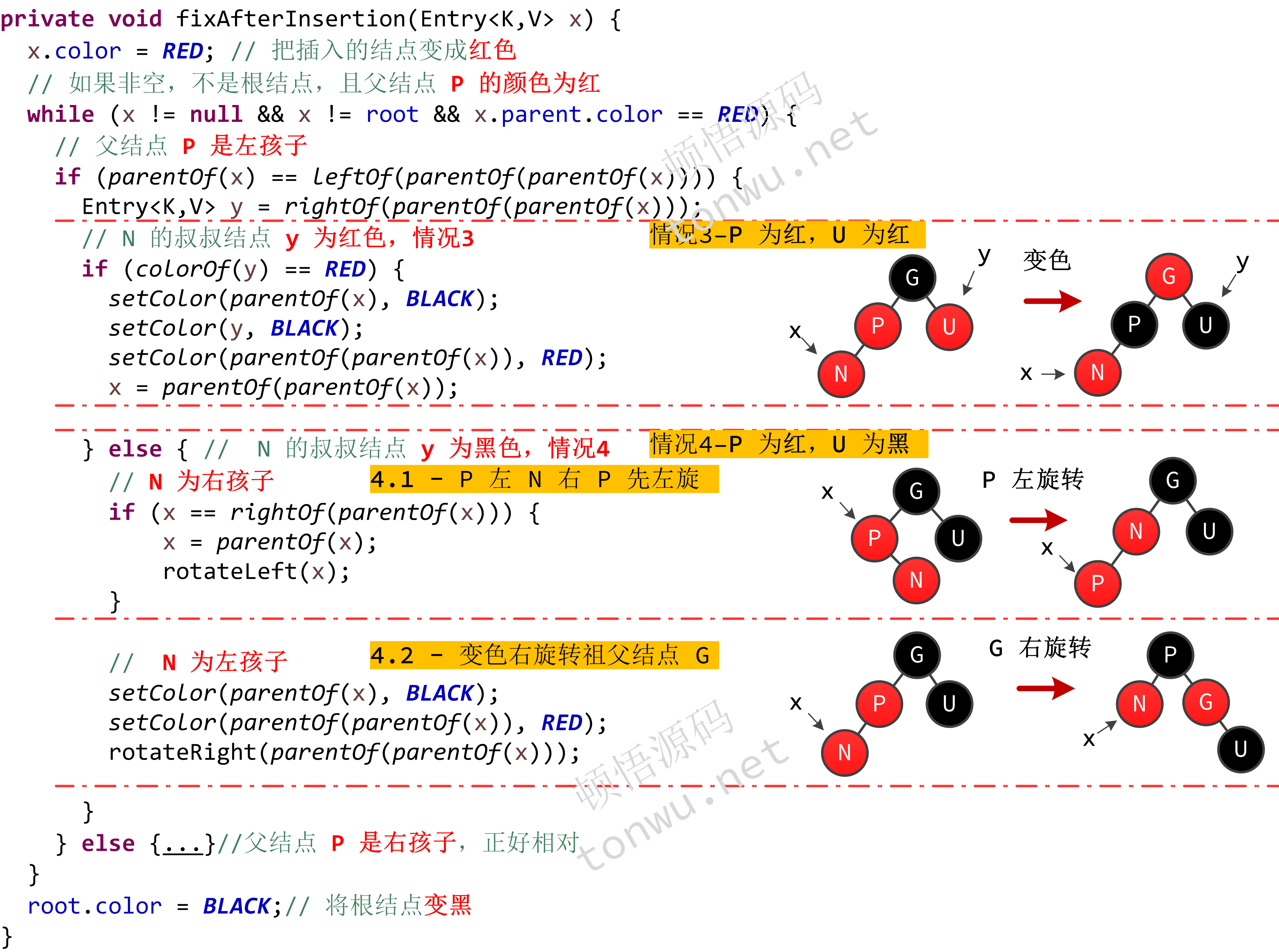
删除

结点的删除也可能会打破红黑树的平衡，相比插入它的情况更复杂，假设待删除结点为 M，如果有非叶子结点，称为 C，那么有两种比较简单的删除情况：

1. M 为红色结点，那么它必是叶子结点，直接删除即可，因为如果它有一个黑色的非叶子结点，那么就违反了性质5，通过 M 向左或向右的路径黑色结点不等
2. M 是黑色而 C 是红色，只需要让 C 替换到 M 的位置，并变成黑色即可，或者说交换 C 和 M 的值，并删除 C（就是第一个简单的情况）

这两个情况，本质都是删除了一个红色结点，不影响整体平衡，比较复杂的是 M 和 C 都是黑色的情况，需要找一个结点填补这个黑色空缺。

结点 M删除后它的位置上就变成了 NIL 隐形结点，为了方便描述，这个结点记为 N，P 表示 N 的父结点，S 表示 N 兄弟结点，S 如果存在左右孩子，分别使用 SL 和 SR 表示，那么删除就有以下几种情况：

1. N 是根结点 - 直接删除即可
2. P 黑 S 红 - 交换 P 和 S 的颜色，然后对 P 左旋转
3. P 黑 S 黑 - 将 S 变成红色，问题递归到父结点处理
4. P 红 S 黑 - 将 S 变成红色，删除成功
5. P 颜色任意 S 黑 SL 红 - 对 S 右旋转，并交换 S 和 SL 的颜色，变成情况6
6. P 颜色任意 S 黑，SR 红 - 对 P 左旋转，交换 P 和 S 的颜色，并将 SR 变成黑色

针对这些情况，TreeMap 进行了实现：

public V remove(Object key) {
  Entry<K,V> p = getEntry(key);// 查找结点
  if (p == null) return null;

  V oldValue = p.value;
  deleteEntry(p); // 删除结点
  return oldValue;
}
private void deleteEntry(Entry<K,V> p) {
  modCount++;
  size--;
  // 如果 p 有两个孩子结点，转成删除最多有一个孩子的结点的情况
  // 这里查找的是 p 的后继结点，也就是右子树值最小的结点
  if (p.left != null && p.right != null) {
    Entry<K,V> s = successor(p); // 查找后继结点
    // 复制后继结点的 key 和 value 到 p
    p.key = s.key;
    p.value = s.value;
    p = s; // 将 p 指向这个右子树值最小的结点
  } // p has 2 children

  // 此时删除的 p 要么是叶子结点，要么只有一个左或右孩子
  Entry<K,V> replacement = (p.left != null ? p.left : p.right);

  if (replacement != null) { // 有孩子结点
    // 有一个左或右孩子，使用这个孩子结点替换它的父结点 p
    replacement.parent = p.parent;
    if (p.parent == null) root = replacement;
    else if (p == p.parent.left)
      p.parent.left  = replacement;
    else
      p.parent.right = replacement;

    // Null out links so they are OK to use by fixAfterDeletion.
    // 删除结点 p，也就是断开所有的链接
    p.left = p.right = p.parent = null;

    // Fix replacement. 如果删除的是黑色结点
    if (p.color == BLACK)
      fixAfterDeletion(replacement); // 平衡调整
  } else if (p.parent == null) { // return if we are the only node.
    root = null;// 情况1，删除后变成空树
  } else {//No children. Use self as phantom replacement and unlink.
    // 删除的是叶子结点，那么删除 p 就是用它的隐形 NIL 叶子结点替换
    // 它，这里将它自己看做隐形的叶子结点
    if (p.color == BLACK)
      fixAfterDeletion(p); //如果是黑色，进行平衡调整
    // 从树中移除 P
    if (p.parent != null) {
      if (p == p.parent.left)
        p.parent.left = null;
      else if (p == p.parent.right)
        p.parent.right = null;
      p.parent = null;
    }
  }
}

deleteEntry 的逻辑就和二叉查找树一样，主要就是把删除任一结点的问题就简化成：删除一个最多只有一个孩子的结点的情况，并且所有的删除操作都在叶子结点完成。如果删除的是黑色结点，那么就视情况调整树重新达到平衡，具体代码如下:

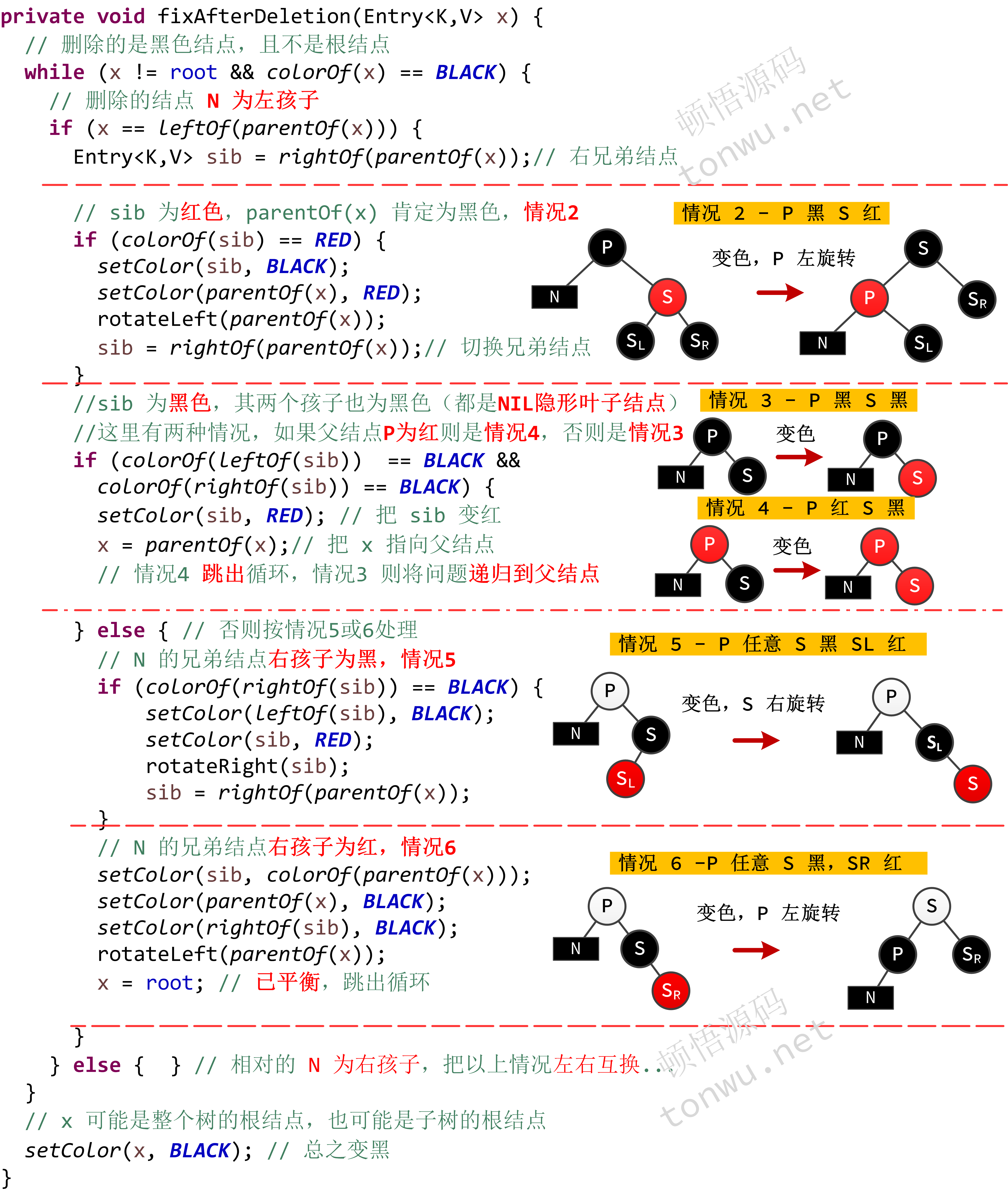
查找

就像二分查找那样，TreeMap 也能在 ~lgN 次比较内结束查找，并且针对 键-key 提供了丰富的查询 API，

• get(Object key) - 返回等于给定键的结点
• floorEntry(K key) - 返回小于或等于给定键的结点中键最大的结点
• ceilingEntry(K key) - 返回大于或等于给定键的结点中键最小的结点
• higherEntry(K key) - 返回严格大于给定键的结点中键最小的结点
• lowerEntry(K key) - 返回严格小于给定键的结点中键最大的结点

上面这些方法比较简单，可自行查看源码。另外，还有两个比较特殊的方法，它们用来查询指定结点在树中序遍历序列中的前驱和后继结点，在中序遍历序列中：

• 前驱结点也就是左子树值最大的结点
• 后继结点也就是右子树值最小的结点

遍历

遍历也是一个高频操作，在 Java 集合框架体系中，基本都是采用迭代器 Iterator 来实现，TreeMap 也是如此，它提供了对键和对值的迭代器。

TreeMap 迭代器最终的逻辑实现是在 PrivateEntryIterator 类中，默认按键的正序输出，它也提供了一个逆序输出的迭代器 DescendingKeyIterator。

具体代码不在贴出，比较简单，值得注意的就是上一节介绍的查找前驱和后继结点的两个方法，遍历常用 API 有：

• entrySet() - 返回一个遍历所有结点的 Set 集合
• keySet() - 返回一个遍历所有键的 Set 集合
• values() - 返回一个遍历所有值的 Set 集合

小结

分析 TreeMap 的源码之前，一定要去分析红黑树的原理，然后在看它的源码，相信理论与实践相结合，掌握红黑树不在话下，TreeMap 也会用得游刃有余。