大疆2019校招FPGA笔试总结

1.对于同步fifo，每100个cycle可以写入80个数据，每10个cycle可以读出8个数据，fifo的深度至少为？

写时钟频率 w_clk,
读时钟频率 r_clk,
写时钟周期里，每B个时钟周期会有A个数据写入FIFO
读时钟周期里，每Y个时钟周期会有X个数据读出FIFO
则，FIFO的最小深度是？

计算公式如下：

fifo_depth = burst_length - burst_length * X/Y * r_clk/w_clk

例举说明：
如果100个写时钟周期可以写入80个数据，10个读时钟可以读出8个数据。令wclk＝rclk ，考虑背靠背（20个clk不发数据＋80clk发数据＋80clk发数据＋20个clk不发数据的200个clk）代入公式可计算FIFO的深度
fifo_depth = 160-160X（80%）=160-128= 32

拓展：
如果令wclk＝200mhz，改为100个wclk里写入40个，rclk＝100mhz，10个rclk里读出8个。那么fifo深度为48
计算如下fifo_depth =-80X（%）X(/)=-=

2.如果只使用2选1mux完成异或逻辑，至少需要几个mux？

一开始想到的答案如下，需要3个，未详加验证：

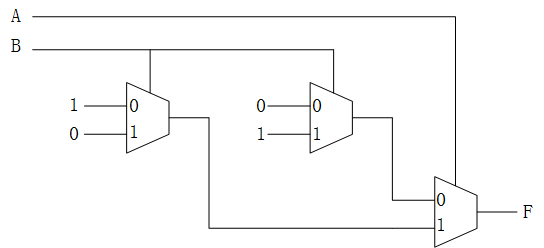
后来经人指正发现确实不太对，纠正为至少需要两个，如下图：

3.在对信号采样过程之前抗混滤波,其作用是什么?它选用何种滤波器?其截止频率如何确定?

根据“奈奎斯特采样定律”：在对模拟信号进行离散化时,采样频率f2至少应2倍于被分析的信号的最高频率f1,即：f2≥ f1；否则可能出现因采样频率不够高,模拟信号中的高频信号折叠到低频段,出现虚假频率成分的现象
但工程测量中采样频率不可能无限高也不需要无限高,因为我们一般只关心一定频率范围内的信号成份.
为解决频率混叠,在对模拟信号进行离散化采集前,采用低通滤波器滤除高于1/2采样频率的频率成份.实际仪器设计中,这个低通滤波器的截止频率(fc) 为：
截止频率（fc）= 采样频率（fz） / 2．56 

4.线与逻辑

线与逻辑是两个输出信号相连可以实现“与”的功能，可以用OC或OD门来实现，需要在输出端加一个上拉电阻。

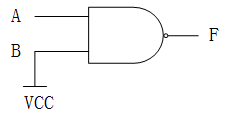
5.将二输入的与非门当非门使用时，另一端的接法应该是

二输入与非门的真值表如下：       非门的真值表如下：

　 　

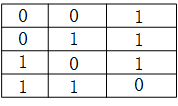
假设现在A端为非门的输入，F为输出。A=0时，B端任意高低电平，F都为1；A=1时，B只有等于1,即接高电平，F才等于1。

所以，最终接法如下：（另一端B接高电平）

6.属于高速串行接口的是

  PCIE,USB,SPI,RapidIO；（abcd）

7.关于芯片启动时初始化代码在调到main函数之前会执行的操作

8.Verilog HDL中哪些结构是不可综合的

　（1）所有综合工具都支持的结构：always，assign，begin，end，case，wire，tri，aupply0，supply1，reg，integer，default，for，function，and，nand，or，nor，xor，xnor，buf，not，bufif0，bufif1，notif0，notif1，if，inout，input，instantitation，module，negedge，posedge，operators，output，parameter。
    （2）所有综合工具都不支持的结构：time，defparam，$finish，fork，join，initial，delays，UDP，wait。
    （3）有些工具支持有些工具不支持的结构：casex，casez，wand，triand，wor，trior，real，disable，forever，arrays，memories，repeat，task，while。

9.关于时序设计和异步设计的描述

10.代码覆盖率

　包括语句覆盖，判定覆盖，条件覆盖，路径覆盖；

11.面积和速度优化

　面积优化：资源共享，逻辑复制，串行化；

　速度优化：流水线，关键路径法，寄存器配平；

12.关于正则表达式中的计数符和通用字符集进行搜索匹配

　　

13.时序检查中对异步复位电路的时序分析叫做（）和（）？

　　这个题做的让人有点懵，我知道异步复位电路一般需要做异步复位、同步释放处理，但不知道这里问的啥意思。

　　这个经指点，应该是恢复时间检查和移除时间检查。

后面能记起来的就是问了一个关于FPGA内部资源包括哪些及其作用，一个通关序列发生器画Moore状态机，还有一个关于系统最大频率计算的。