[数据结构] 2.7 Heap 堆

* 注: 本文/本系列谢绝转载，如有转载，本人有权利追究相应责任。

1.堆是什么？

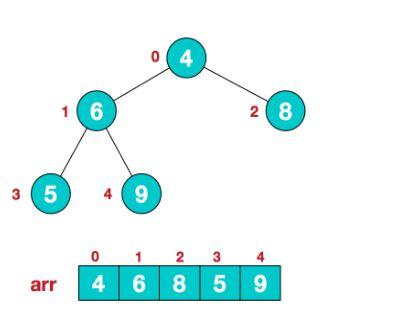
（如图所示是一个小堆）

1)堆是一颗完全二叉树，它的最后一层不是满的，其他每一层都是满的，最后一层从左到右也没有空隙。

　简单的说?  完全二叉树也就是没有缝隙的二叉树。

2)堆常常通过数组实现，因为 父子节点直接的关系直接可以通过数组的索引换算

　　parent(i) = i/2

　　left child(i) = 2*i + 1

　　right child(i) = 2*i + 2

3)对于最大堆来说，每个节点的值都不大于其父节点的值，也就是根节点是最大的。

　对于最小堆来说，每个节点的值都不小于其父节点的值，也就是根节点是最小的

4)堆进行插入和删除的时间复杂度均为 O(LogN)

2.堆的应用

堆可以解决的首先就是topK问题，假设要从N大小的实数数组中找到topK，那么需要K*logN的时间。

当N=10000时

当N=10000*10000时

也就是说N可以放的足够大，K可以适当大一些，经过本机实验，堆在单机单线程下只需要14s就可以处理一亿数据的Top1W操作。

3.堆的实现

堆的操作主要是两个 add、remove，有些地方也会存在buildHeap的操作，我们分别捋一下它们的思路。

一下基于一个最大堆。

1) add操作，添加元素

思路:

将添加的元素放在数组尾部，进行“上浮”操作。也就是比较父元素，如果大于父元素则上浮。

实际长度 ++

        /**
         * 插入过程需要上浮比较
         * @param node
         */
        public void insert(Node node){
            if(actualSize == MAX_N){
                System.out.println("当前堆已满!");
                return;
            }

            // 插入
            // 插入节点
            nodes[actualSize] = node;

            // 上浮过程
            // 调整堆，从这个节点开始与其夫节点进行比较，如果大于父节点则交换上浮
            for(int i = actualSize; i > 0 ;i = getParentIndex(i)){
                Node current = nodes[i];
                Node parent = nodes[getParentIndex(i)];
                if(parent.data < current.data){
                    nodes[i] = parent;
                    nodes[getParentIndex(i)] = current;
                }
            }
            actualSize ++;
        }

2) remove操作，删除元素

思路:

获得堆顶的值，然后用堆底节点替换堆顶节点。并针对此节点进行"下沉"操作，所谓下沉，就是如果比较当前元素与左右子节点的值，如果比它们小，则与最大者交换。

实际长度 --

 /**
         * 删除过程需要下沉比较
         * @param node
         */
        public void remove(Node node){
            if(actualSize == 0){
                System.out.println("当前堆已空!");
                return;
            }

            if(actualSize == 1){
               actualSize --;
               return;
            }

            // 删除过程
            // 使用最后一个节点替换掉顶点
            Node tailNode = nodes[actualSize-1];
            nodes[0] = tailNode;
            actualSize --;

            // 下沉比较
            for(int i = 0; i < actualSize;){
                Node current = nodes[i];

                Node leftChild = null;
                if(getLeftChildIndex(i) < actualSize){
                   leftChild = nodes[getLeftChildIndex(i)];
                }
                Node rightChild = null;
                if(getRightChildIndex(i) < actualSize){
                    rightChild = nodes[getRightChildIndex(i)];
                }

                if(leftChild == null && rightChild == null){
                    return;
                }

                if(leftChild != null && leftChild.data > current.data){
                    if(rightChild != null && rightChild.data > leftChild.data){ // 右枝最大
                        nodes[i] = rightChild;
                        nodes[getRightChildIndex(i)] = current;
                        // i走右枝
                        i = getRightChildIndex(i);
                        continue;
                    }else{ // 左枝最大
                        nodes[i] = leftChild;
                        nodes[getLeftChildIndex(i)] = current;
                        // i走左枝
                        i = getLeftChildIndex(i);
                        continue;
                    }
                }else{
                    if(rightChild != null && rightChild.data > current.data){ // 右枝最大
                        nodes[i] = rightChild;
                        nodes[getRightChildIndex(i)] = current;
                        // i走右枝
                        i = getRightChildIndex(i);
                        continue;
                    }else if(rightChild != null && rightChild.data <= current.data){ // 当前点最大
                        //保持现状,直接结束循环
                        break;
                    }
                }
            }
        }

3)buildHeap操作，给一个数组，进行建立堆操作

思路:

　　遍历数组的每一个节点，针对每个节点进行"上浮"操作.

Code：

package ds6.heap;

import java.util.Arrays;

public class Heap {
    static class Node{
        long data;

        public Node(long data) {
            this.data = data;
        }

        @Override
        public String toString() {
            return "Node{" +
                    "data=" + data +
                    '}';
        }
    }

    /**
     * TopN最大值堆
     */
    static class TopNMaxHeap{
        int MAX_N = 10; // Top N ,指定堆的最大大小
        Node[] nodes;
        int actualSize = 0;

        public TopNMaxHeap(int MAX_N) {
            this.MAX_N = MAX_N;
            nodes = new Node[MAX_N];
        }

        public void foreachPrint(){
            System.out.println(Arrays.toString(nodes));
        }

        /**
         * 删除过程需要下沉比较
         * @param node
         */
        public void remove(Node node){
            if(actualSize == 0){
                System.out.println("当前堆已空!");
                return;
            }

            if(actualSize == 1){
               actualSize --;
               return;
            }

            // 删除过程
            // 使用最后一个节点替换掉顶点
            Node tailNode = nodes[actualSize-1];
            nodes[0] = tailNode;
            actualSize --;

            // 下沉比较
            for(int i = 0; i < actualSize;){
                Node current = nodes[i];

                Node leftChild = null;
                if(getLeftChildIndex(i) < actualSize){
                   leftChild = nodes[getLeftChildIndex(i)];
                }
                Node rightChild = null;
                if(getRightChildIndex(i) < actualSize){
                    rightChild = nodes[getRightChildIndex(i)];
                }

                if(leftChild == null && rightChild == null){
                    return;
                }

                if(leftChild != null && leftChild.data > current.data){
                    if(rightChild != null && rightChild.data > leftChild.data){ // 右枝最大
                        nodes[i] = rightChild;
                        nodes[getRightChildIndex(i)] = current;
                        // i走右枝
                        i = getRightChildIndex(i);
                        continue;
                    }else{ // 左枝最大
                        nodes[i] = leftChild;
                        nodes[getLeftChildIndex(i)] = current;
                        // i走左枝
                        i = getLeftChildIndex(i);
                        continue;
                    }
                }else{
                    if(rightChild != null && rightChild.data > current.data){ // 右枝最大
                        nodes[i] = rightChild;
                        nodes[getRightChildIndex(i)] = current;
                        // i走右枝
                        i = getRightChildIndex(i);
                        continue;
                    }else{ // 当前点最大
                        //保持现状,直接结束循环
                        break;
                    }
                }
            }
        }

        /**
         * 插入过程需要上浮比较
         * @param node
         */
        public void insert(Node node){
            if(actualSize == MAX_N){
                System.out.println("当前堆已满!");
                return;
            }

            // 插入
            // 插入节点
            nodes[actualSize] = node;

            // 上浮过程
            // 调整堆，从这个节点开始与其夫节点进行比较，如果大于父节点则交换上浮
            for(int i = actualSize; i > 0 ;i = getParentIndex(i)){
                Node current = nodes[i];
                Node parent = nodes[getParentIndex(i)];
                if(parent.data < current.data){
                    nodes[i] = parent;
                    nodes[getParentIndex(i)] = current;
                }
            }
            actualSize ++;
        }

        public int getParentIndex(int x){
            return (x-1)/2;
        }

        public int getLeftChildIndex(int x){
            return 2*x + 1;
        }

        public int getRightChildIndex(int x){
            return 2*x + 2;
        }
    }

    public static void main(String[] args) {
        TopNMaxHeap topNMaxHeap = new TopNMaxHeap(10);
        topNMaxHeap.insert(new Node(27));
        topNMaxHeap.insert(new Node(33));
        topNMaxHeap.insert(new Node(30));
        topNMaxHeap.insert(new Node(31));
        Node nodeToRemove = new Node(40);
        topNMaxHeap.insert(nodeToRemove);
        topNMaxHeap.insert(new Node(20));
        topNMaxHeap.foreachPrint();
        topNMaxHeap.remove(nodeToRemove);
        topNMaxHeap.foreachPrint();
    }

}

result:

[Node{data=40}, Node{data=33}, Node{data=30}, Node{data=27}, Node{data=31}, Node{data=20}, null, null, null, null]
[Node{data=33}, Node{data=31}, Node{data=30}, Node{data=27}, Node{data=20}, Node{data=20}, null, null, null, null]

4.堆排序

因为堆的这个特性，通过不断poll出堆顶元素就可以对元素列表进行排序。

测试:

    public static void test2(){
        int[] toSort = new int[]{
                7,10,6,8,9,3,5,4
        };

        TopNMaxHeap heap = new TopNMaxHeap(toSort.length);
        for(int i = 0 ; i < toSort.length; i++ ){
            heap.insert(new Node(toSort[i]));
        }

        int[] result = new int[toSort.length];
        for(int i = 0; i < toSort.length; i++ ){
            result[i]=(int)heap.nodes[0].data;
            heap.remove(heap.nodes[0]);
        }

        System.out.println(Arrays.toString(result));

    }

result:

[10, 9, 8, 7, 6, 5, 4, 3]