P1744 采购特价商品题解(讲解图论)

图论的超级初级题目（模板题）

最短路径的模板题

图是啥？（白纸上的符号？）

对于一个拥有n个顶点的无向连通图，它的边数一定多于n-1条。若从中选择n-1条边，使得无向图仍然连通，则由n个顶点及这 n-1条边（弧）组成的图被称为原无向图的生成树。

换句话说，有边有点就是图。（本蒟蒻的理解是这样。。QWQ）

另外，还有一些与图有关的定义（很好理解，通俗一点）：

阶：图中点的个数。

边：两个点间的连接

权值：边的长度

。。。想了解更多找度娘，她可能讲的比我通俗QWQ。

邻接矩阵：

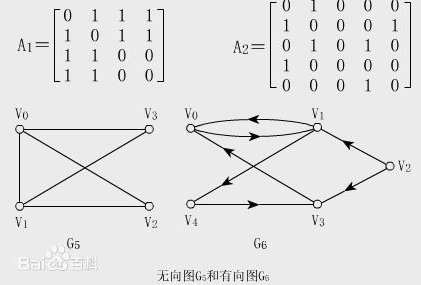
进入正题：

题目背景

《爱与愁的故事第三弹·shopping》第一章。

题目描述

中山路店山店海，成了购物狂爱与愁大神的“不归之路”。中山路上有n（n<=100）家店，每家店的坐标均在-10000~10000之间。其中的m家店之间有通路。若有通路，则表示可以从一家店走到另一家店，通路的距离为两点间的直线距离。现在爱与愁大神要找出从一家店到另一家店之间的最短距离。你能帮爱与愁大神算出吗？

输入输出格式

输入格式：

共n+m+3行：

第1行：整数n

第2行~第n+1行：每行两个整数x和y，描述了一家店的坐标

第n+2行：整数m

第n+3行~第n+m+2行：每行描述一条通路，由两个整数i和j组成，表示第i家店和第j家店之间有通路。

第n+m+3行：两个整数s和t，分别表示原点和目标店

输出格式：

仅一行：一个实数（保留两位小数），表示从s到t的最短路径长度。

输入输出样例

输入样例#1：复制

输出样例#1：复制

3.41

说明

100%数据：n<=100，m<=1000

先预处理转化为邻接矩阵后再直接输出就可以了

具体算法为Floyd算法

上AC代码：

#include<cstdio>

#include<cstring>

#include<cmath>

#include<iostream>

using namespace std;

int n,m,a[][],e,g,aa,bb;//a用来存x，y坐标

double f[][];//f用来存路径的

int main(){

    scanf("%d",&n);

    for(int i=;i<=n;i++)

        cin>>a[i][]>>a[i][];  //scanf("%d%d",&a[i][0],&a[i][1]);

    scanf("%d",&m);

    memset(f,0x7f,sizeof(f));

    for(int i=;i<=m;i++)

    {

        scanf("%d%d",&e,&g);//代替x，y ，因为cmath中有x，y了（真的很无语啊）

        f[g][e]=sqrt(pow(double(a[e][]-a[g][]),)+pow(double(a[e][]-a[g][]),));

        f[e][g]=sqrt(pow(double(a[e][]-a[g][]),)+pow(double(a[e][]-a[g][]),));

    }

    scanf("%d%d",&aa,&bb);

    for(int k=;k<=n;k++)//开启O（n^3）暴力模式——

        for(int i=;i<=n;i++)

            for(int j=;j<=n;j++)

            {

                if((i!=j)&&(i!=k)&&(j!=k)&&(f[i][j]>(f[i][k]+f[k][j])))

                    f[i][j]=f[i][k]+f[k][j];

            }

    printf("%0.2lf",f[aa][bb]);//暴力过后松一口气，直接输出您想要的点就行了

    return ;

}

完结✿ヽ(°▽°)ノ✿

希望对大家有所帮助