机器学习--PCA降维和Lasso算法

1、PCA降维

降维有什么作用呢？
数据在低维下更容易处理、更容易使用；
相关特征，特别是重要特征更能在数据中明确的显示出来；如果只有两维或者三维的话，更便于可视化展示；
去除数据噪声
降低算法开销

常见的降维算法有主成分分析（principal component analysis,PCA）、因子分析（Factor Analysis）和独立成分分析（Independent Component Analysis，ICA），其中PCA是目前应用最为广泛的方法。

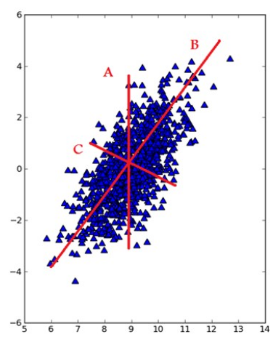
在PCA中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个坐标轴的选择是原始数据中方差最大的方向，从数据角度上来讲，这其实就是最重要的方向，

即下图总直线B的方向。第二个坐标轴则是第一个的垂直或者说正交（orthogonal）方向，即下图中直线C的方向。该过程一直重复，重复的次数为原始数据中特征的数目。

而这些方向所表示出的数据特征就被称为“主成分”。

Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，

以此使用较少的数据维度，同时保留住较多的原数据点的特性。

通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是PCA并不试图去探索数据内在结构）

2、Lasso算法

参考自：http://blog.csdn.net/slade_sha/article/details/53164905

先看一波过拟合：

图中，红色的线存在明显的过拟合，绿色的线才是合理的拟合曲线，为了避免过拟合，我们可以引入正则化。

下面可以利用正则化来解决曲线拟合过程中的过拟合发生，存在均方根误差也叫标准误差，即为√[∑di^2/n]=Re，n为测量次数；di为一组测量值与真值的偏差。

实际考虑回归的过程中，我们需要考虑到误差项，

这个和简单的线性回归的公式相似，而在正则化下来优化过拟合这件事情的时候，会加入一个约束条件，也就是惩罚函数：

这边这个惩罚函数有多种形式，比较常用的有l1,l2，大概有如下几种：

讲一下比较常用的两种情况，q＝1和q＝2的情况：

q＝1，也就是今天想讲的lasso回归，为什么lasso可以控制过拟合呢，因为在数据训练的过程中，可能有几百个，或者几千个变量，再过多的变量衡量目标函数的因变量的时候，可能造成结果的过度解释，而通过q＝1下的惩罚函数来限制变量个数的情况，可以优先筛选掉一些不是特别重要的变量，见下图：

作图只要不是特殊情况下与正方形的边相切，一定是与某个顶点优先相交，那必然存在横纵坐标轴中的一个系数为0，起到对变量的筛选的作用。

q＝2的时候，其实就可以看作是上面这个蓝色的圆，在这个圆的限制下，点可以是圆上的任意一点，所以q＝2的时候也叫做岭回归，岭回归是起不到压缩变量的作用的，在这个图里也是可以看出来的。

lasso回归：

lasso回归的特色就是在建立广义线型模型的时候，这里广义线型模型包含一维连续因变量、多维连续因变量、非负次数因变量、二元离散因变量、多元离散因变，除此之外，无论因变量是连续的还是离散的，lasso都能处理，总的来说，lasso对于数据的要求是极其低的，所以应用程度较广；除此之外，lasso还能够对变量进行筛选和对模型的复杂程度进行降低。这里的变量筛选是指不把所有的变量都放入模型中进行拟合，而是有选择的把变量放入模型从而得到更好的性能参数。 复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过度拟合(Overfitting)。 对于线性模型来说，复杂度与模型的变量数有直接关系，变量数越多，模型复杂度就越高。 更多的变量在拟合时往往可以给出一个看似更好的模型，但是同时也面临过度拟合的危险。

lasso的复杂程度由λ来控制，λ越大对变量较多的线性模型的惩罚力度就越大，从而最终获得一个变量较少的模型。除此之外，另一个参数α来控制应对高相关性(highly correlated)数据时模型的性状。 LASSO回归α=1，Ridge回归α=0，这就对应了惩罚函数的形式和目的。