SQL serve 数据库--视图、事物、分离附加、备份还原

视图是数据库中的一种虚拟表，与真实的表一样，视图包含一系列带有名称的行和列数据。行和列数据用来自定义视图的查询所引用的表，并且在引用视图时动态生成。

 视图只能用来查询，不能增删改；不允许出现重复列

1. 视图的概念

　　视图是从一个或者多个表中导出的，其行为与表相似，但视图是一个虚拟表。视图可以在已经存在的视图的基础上定义。在视图上用户可以使用SELECT语句查询数据库，使用INSERT、UPDATE和DELETE语句修改记录。对于视图的操作最终转化为对基本数据表的操作。

2. 创建视图

　　使用T-SQL创建视图语法：

create view student11 --视图名
as
select score.sno, sname, sbirthday, score.cno, cname, DEGREE from student,score,course --视图内容
select * from student11 -- 查询视图

　实例：　单表视图

CREATE VIEW [V_Product]
AS
    SELECT [ProductID],[ProductName]
    FROM [dbo].[Product]

　　多表视图

CREATE VIEW [dbo].[V_ProductCategory]
AS
    SELECT [ProductID],[CategoryName],[ProductName]
    FROM [dbo].[Product] INNER JOIN [dbo].[Category]
    ON [dbo].[Product].[CategoryID] = [dbo].[Category].[CategoryID]

　　创建排序视图

CREATE VIEW [dbo].[V_Product]
AS
    SELECT TOP 100 PERCENT [ProductID],[ProductName]
    FROM [dbo].[Product]
    ORDER BY [UnitPrice]

3. 修改视图

鼠标放在视图名——右键——设计——

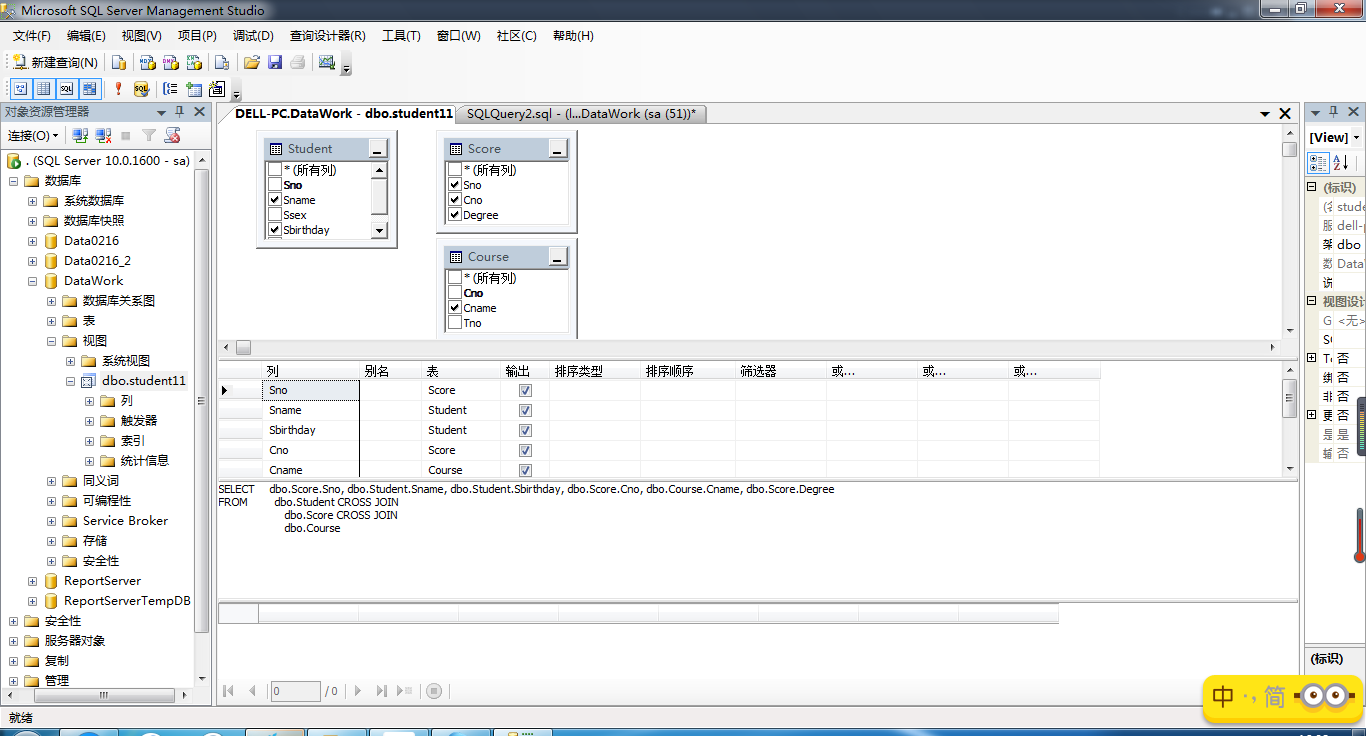
4. 查看视图

　　查看视图结构：

EXEC sp_help [V_Product]

　　查看视图文本：

EXEC sp_helptext [V_Product]

5. 删除视图

　　删除单个视图：

DROP VIEW [V_Product]

　　删除多个视图：

DROP VIEW [V_Product],[V_ProductCategory]

事物：

• Begin Transaction：标记事务开始。
• Commit Transaction：事务已经成功执行，数据已经处理妥当。
• Rollback Transaction：数据处理过程中出错，回滚到没有处理之前的数据状态，或回滚到事务内部的保存点。
• Save Transaction：事务内部设置的保存点，就是事务可以不全部回滚，只回滚到这里，保证事务内部不出错的前提下。
• 格式：
• begin tran
• select * from user
• if @@error >0
• begin
• rollback tran ;
• end
• else
• begin
• commit tran
• end

在一个事务中，你写啦2条sql语句，一条是修改订单表状态,一条是修改库存表库存-1 。 如果在修改订单表状态的时候出错，事务能够回滚，数据将恢复到没修改之前的数据状态，下面的修改库存也就不执行，这样确保你关系逻辑的一致，安全。。

事务就是这个样子,要么全部执行，要么全部不执行，回到原数据状态。

事务具有的特性

• 原子性：事务必须是一个自动工作的单元，要么全部执行，要么全部不执行。
• 一致性：事务结束的时候，所有的内部数据都是正确的。
• 隔离性：并发多个事务时，各个事务不干涉内部数据，处理的都是另外一个事务处理之前或之后的数据。
• 持久性：事务提交之后，数据是永久性的，不可再回滚。