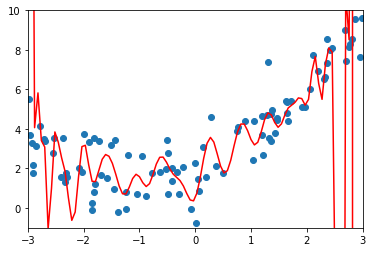
机器学习：模型泛化（岭回归：Ridge Regression）

一、基础理解

　　模型正则化（Regularization）

　　　　# 有多种操作方差，岭回归只是其中一种方式；

• 功能：通过限制超参数大小，解决过拟合或者模型含有的巨大的方差误差的问题；

• 影响拟合曲线的两个因子

1. 模型参数 θ_i （1 ≤ i ≤ n）：决定拟合曲线上下抖动的幅度；
2. 模型截距 θ₀：决定整体拟合曲线上下位置的高低；

二、岭回归

• 岭回归（Ridge Regression）：模型正则化的一种方式；
• 

• 解决的问题：模型过拟合；

• 思路：拟合曲线上下抖动的幅度主要受模型参数的影响，限制参数的大小可以限制拟合曲线抖动的幅度；

　1）原理及操作

• 

• 思路（以多项式回归为例）：在原来的损失函数中加入一个含有所有变量的代数式，此时如果想让目标函数尽可能的小，也必须考虑让所有的参数 θ_i² 尽可能的小，进而可以降低拟合曲线上下的抖动幅度；

　2）公式推导

• 
• 加入的模型正则化：；

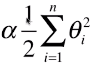1. θ_i ：决定拟合曲线的每一部分的抖动幅度，其中 i 取值范围 1 ~ n ，不包含 0，因为 θ₀ 表示模型的截距；
2. θ₀ ：决定拟合曲线整体的上下位置的高低；
3. 1/2 ：方便计算，因为对式子求导后 θ_i² 变成  2θ_i ，产生的系数 2 刚好与 1/2 相乘为 1；但由于有 α 的存在，1/2 加与不加都没关系；
4. α ：引入的新的超参数，平衡新的损失函数中两部分的关系；是代数式的系数，代表在模型正则化下新的损失函数中，让每一个 θ_i 都尽可能的小，这个小的程度占整个优化损失函数程度的多少；

• 如果 α = 0：表示目标函数中没有加入模型正则化；
• 如果 α = +∞ ：目标函数的另一部分 MSE 占整个目标函数的比重非常的小，主要的优化任务就是让每一个 θ_i 都尽可能的小；

三、实例查看岭回归对模型的影响

　1）模拟数据集

• import numpy as np
  import matplotlib.pyplot as plt
  
  np.random.seed(42)
  # np.random.uniform(-3, 3, size=100)：在 [-3, 3] 之间等分取 100 个数；
  x = np.random.uniform(-3.0, 3.0, size=100)
  X = x.reshape(-1, 1)
  y = 0.5 * x + 3. + np.random.normal(0, 1, size=100)
  
  plt.scatter(x, y)
  plt.show()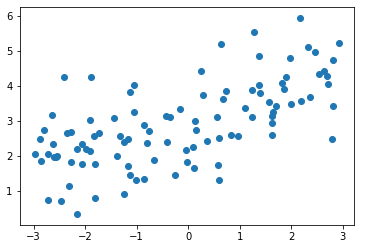

  

　2）使用多形式回归过拟合数据

• 使用管道的方式使用多项式回归

  from sklearn.pipeline import Pipeline
  from sklearn.preprocessing import PolynomialFeatures
  from sklearn.preprocessing import StandardScaler
  from sklearn.linear_model import LinearRegression
  
  # 使用多项式回归的管道方法
  def PolynomialRegression(degree):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('lin_reg', LinearRegression())
      ])
  
  from sklearn.model_selection import train_test_split
  
  np.random.seed(666)
  X_train, X_test, y_train, y_test = train_test_split(X, y)
  
  from sklearn.metrics import mean_squared_error
  
  poly_reg = PolynomialRegression(degree=20)
  poly_reg.fit(X_train, y_train)
  
  y_poly_predict = poly_reg.predict(X_test)
  mean_squared_error(y_test, y_poly_predict)
  # 输出：167.9401086729357

  # 均方误差：167.9401086729357

• 绘制模型曲线

  # np.linspace(-3, 3, 100)：在 [-3, 3] 之间等分取 100 个数，包含 -3 和 3；
  X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
  y_plot = poly_reg.predict(X_plot)
  
  plt.scatter(x, y)
  plt.plot(X_plot[:, 0], poly_reg.predict(X_plot), color='r')
  plt.axis([-3, 3, 0, 6])
  plt.show()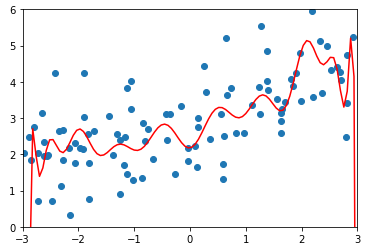

  

　3）使用岭回归

• from sklearn.linear_model import Ridge

• 将绘图代码封装为一个函数

  def plot_model(model):
      X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
      y_plot = model.predict(X_plot)
  
      plt.scatter(x, y)
      plt.plot(X_plot[:, 0], model.predict(X_plot), color='r')
      plt.axis([-3, 3, 0, 6])
      plt.show()

• 使用管道的方式使用岭回归方法

  from sklearn.linear_model import Ridge
  
  def RidgeRegression(degree, alpha):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('ridge_reg', Ridge(alpha=alpha))
      ])

• degree = 20、α = 0.0001

  ridge1_reg = RidgeRegression(20, 0.0001)
  ridge1_reg.fit(X_train, y_train)
  
  y1_predict = ridge1_reg.predict(X_test)
  mean_squared_error(y_test, y1_predict)
  # 输出：1.323349275406402（均方误差）
  
  plot_model(ridge1_reg)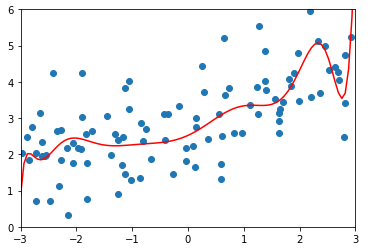

  

• degree = 20、α = 1

  ridge2_reg = RidgeRegression(20, 1)
  ridge2_reg.fit(X_train, y_train)
  
  y2_predict = ridge2_reg.predict(X_test)
  mean_squared_error(y_test, y2_predict)
  # 输出：1.1888759304218448（均方误差）
  
  plot_model(ridge2_reg)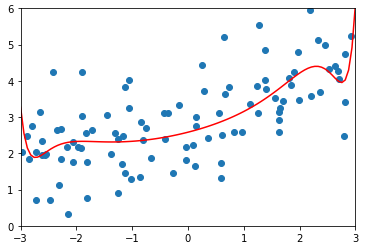

  

• degree = 20、α = 100

  ridge3_reg = RidgeRegression(20, 100)
  ridge3_reg.fit(X_train, y_train)
  
  y3_predict = ridge3_reg.predict(X_test)
  mean_squared_error(y_test, y3_predict)
  # 输出：1.3196456113086197（均方误差）
  
  plot_model(ridge3_reg)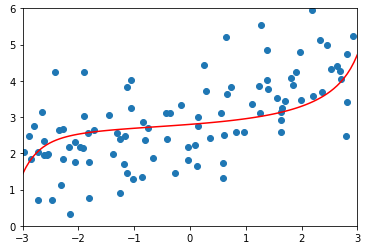

  

• degree=20、alpha=1000000（相当于无穷大）

  ridge4_reg = RidgeRegression(20, 1000000)
  ridge4_reg.fit(X_train, y_train)
  
  y4_predict = ridge4_reg.predict(X_test)
  mean_squared_error(y_test, y4_predict)
  # 输出：1.8404103153255003
  
  plot_model(ridge4_reg)

  

• 当 α = 1000000（相当于无穷大）时：拟合曲线几乎是一条水平的直线，因为当 α 非常大的时候，对目标函数的影响相当于只有添加的模型正则化在起作用；