P4196 [CQOI2006]凸多边形 半平面交

\(\color{#0066ff}{题目描述}\)

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：

则相交部分的面积为5.233。

\(\color{#0066ff}{输入格式}\)

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数mi，表示多边形的边数，以下mi行每行两个整数，逆时针给出各个顶点的坐标。

\(\color{#0066ff}{输出格式}\)

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

\(\color{#0066ff}{输入样例}\)

2
6
-2 0
-1 -2
1 -2
2 0
1 2
-1 2
4
0 -3
1 -1
2 2
-1 0

\(\color{#0066ff}{输出样例}\)

5.233

\(\color{#0066ff}{数据范围与提示}\)

100%的数据满足：2<=n<=10，3<=mi<=50，每维坐标为[-1000,1000]内的整数

\(\color{#0066ff}{题解}\)

半平面交裸题

开两个结构体储存点和线

根据输入方式，自己定义直线方向，那么半平面的方向就确定了

代码中规定的方向是向量左边

两个向量求交(\(AC, BE\))

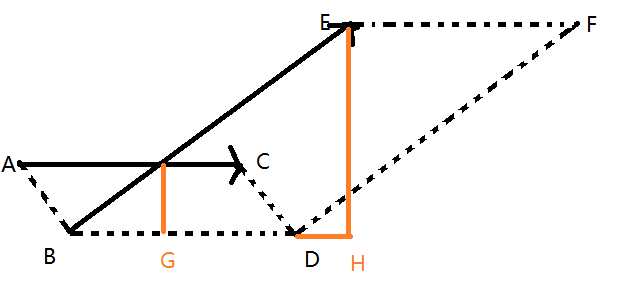
做出这样的平行四边形

过E作EH，过p（交点）作PG

显然BPG，BEH相似，而且作的两条线为平行四边形的高

又因为两个平行四边形的底相等

所以高之比等于相似比?

通过叉积可以获得面积比（相似比）

然后\(p = B + k * v_2\)

以上为向量求交点

我们维护一个双端队列

每次来一跳新的直线，把收到影响的队首，队尾弹出

最后队列里就是有效直线

把相邻的交点都求出来，那么这个多边形的面积就是半平面交的面积

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL in() {
	char ch; int x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 505;
double eps = 1e-8;
int T(double x) {
	if(x > eps) return 1;
	if(x < -eps) return -1;
	return 0;
}
struct node {
	double x, y;
	node(double x = 0, double y = 0): x(x), y(y) {}
	node operator + (const node &b) const {
		return node(x + b.x, y + b.y);
	}
	node operator - (const node &b) const {
		return node(x - b.x, y - b.y);
	}
	double operator ^ (const node &b) const {
		return x * b.y - y * b.x;
	}
	double jj() const {
		return atan2(y, x);
	}
	node operator * (double b) const {
		return node(x * b, y * b);
	}
}e[maxn];

struct line {
	node from, to;
	line(node from = node(), node to = node()): from(from), to(to) {}
	double jj() const {
		return (to - from).jj();
	}
	bool operator < (const line &b) const {
		return T(jj() - b.jj()) == 0? T((to - from) ^ (b.to - from)) > 0 : T(jj() - b.jj()) < 0;
	}
}a[maxn], q[maxn];
int n, head, tail, ji;
node to(line i, line j) {
	node x = i.to - i.from, y = j.to - j.from, z = j.from - i.from;
	return j.from + y * ((z ^ x) / (x ^ y));
}
bool jud(line x, line y, line z) {
	node p = to(x, y);
	return ((z.to - z.from) ^ (p - z.from)) < 0;
}
void work() {
	std::sort(a + 1, a + ji + 1);
	int cnt = 0;
	for(int i = 1; i <= ji; i++) {
		if(T(a[i].jj() - a[i - 1].jj())) cnt++;
		a[cnt] = a[i];
	}
	head = 1, tail = 0;
	q[++tail] = a[1], q[++tail] = a[2];
	for(int i = 3; i <= cnt; i++) {
		while(head < tail && jud(q[tail - 1], q[tail], a[i])) tail--;
		while(head < tail && jud(q[head + 1], q[head], a[i])) head++;
		q[++tail] = a[i];
	}
	while(head < tail && jud(q[tail - 1], q[tail], q[head])) tail--;
	while(head < tail && jud(q[head + 1], q[head], q[tail])) head++;
	q[tail + 1] = q[head];
	ji = 0;
	for(int i = head; i <= tail; i++) e[++ji] = to(q[i], q[i + 1]);
}

int main() {
	n = in();
	for(int i = 1; i <= n; i++) {
		int F = in();
		for(int j = 1; j <= F; j++)
			e[j].x = in(), e[j].y = in();
		e[F + 1] = e[1];
		for(int j = 1; j <= F; j++) a[++ji] = line(e[j], e[j + 1]);
	}
	work();
	double ans = 0;
	e[ji + 1] = e[1];
	if(ji > 2) for(int i = 1; i <= ji; i++) ans += (e[i] ^ e[i + 1]);
	printf("%.3f", fabs(ans) / 2.0);
	return 0;
}